深入解读 RL's Razor：为何在线强化学习能有效缓解灾难性遗忘？

当我们使用新数据对大模型进行微调（Fine-tuning）时，模型在获得新能力的同时，往往会严重损害甚至完全忘记之前已经掌握的知识和技能。这就是灾难性遗忘（Catastrophic Forgetting），这一现象限制了模型持续进化的可能性。

监督微调（Supervised Fine-Tuning, SFT）和基于人类反馈的强化学习（Reinforcement Learning from Human Feedback, RLHF）是最主流的两种范式。一个有趣的经验性观察是，尽管两种方法都旨在让模型适应新任务，但研究人员和工程师们发现，与 SFT 相比，RL 微调似乎能更好地保留模型的通用能力，即“遗忘得更少”。

这引出了一个根本性的问题：为什么强化学习（RL）在学习新任务时，其遗忘程度会显著低于监督微调（SFT）？ 这种现象背后的底层机制是什么？

来自 MIT Improbable AI Lab 的 Idan Shenfeld、Jyothish Pari 和 Pulkit Agrawal 最近发表了一篇题为 《RL's Razor: Why Online Reinforcement Learning Forgets Less》 的论文，系统性地回答了这个问题。他们不仅通过大量实验证实了这一现象，更进一步提出了一个简洁而深刻的解释，并将其命名为 “RL's Razor”（RL的剃刀）。

本文将对这篇重要的工作进行深入解读，着重探讨以下几个关键问题：

RL 和 SFT 在学习与遗忘的权衡上表现如何？
究竟是什么因素决定了模型在微调过程中的遗忘程度？
“RL's Razor” 原理的具体内容是什么？
为什么 RL 天然地遵循这一原理，而 SFT 则不然？

核心观点：RL 的奥卡姆剃刀 (RL's Razor)

在深入细节之前，我们首先来理解这篇论文最核心的观点——“RL's Razor”。这个名字致敬了著名的“奥卡姆剃刀”（Occam's Razor）原理，即“如无必要，勿增实体”。奥卡姆剃刀主张在所有能够解释现象的假设中，我们应该选择最简单的那一个。

作者们将这个哲学思想巧妙地迁移到了模型学习的领域。对于一个给定的新任务，通常存在许多种不同的策略（policies）或模型参数配置，它们都能成功地完成这个任务。例如，对于一个数学问题，模型可以给出简短的答案，也可以给出详尽的推导过程，两者都可能得到正确结果。那么，在众多“正确答案”中，模型应该学习哪一个呢？

论文提出的 RL's Razor 原理指出：

在所有能够解决新任务的策略中，强化学习（RL）天然地偏好于那个与原始基础模型在 KL 散度（Kullback-Leibler Divergence）上最接近的解。

换句话说，RL 会寻找一条“阻力最小”的路径来学习新技能。它倾向于在原始模型能力的基础上进行最小程度的修正，以满足新任务的要求。这种内在的“保守性”或者说对“简单解”（即与初始状态最接近的解）的偏好，正是 RL 能够更好地保留先前知识的关键。

我们可以通过论文中的示意图来直观地理解这个概念。

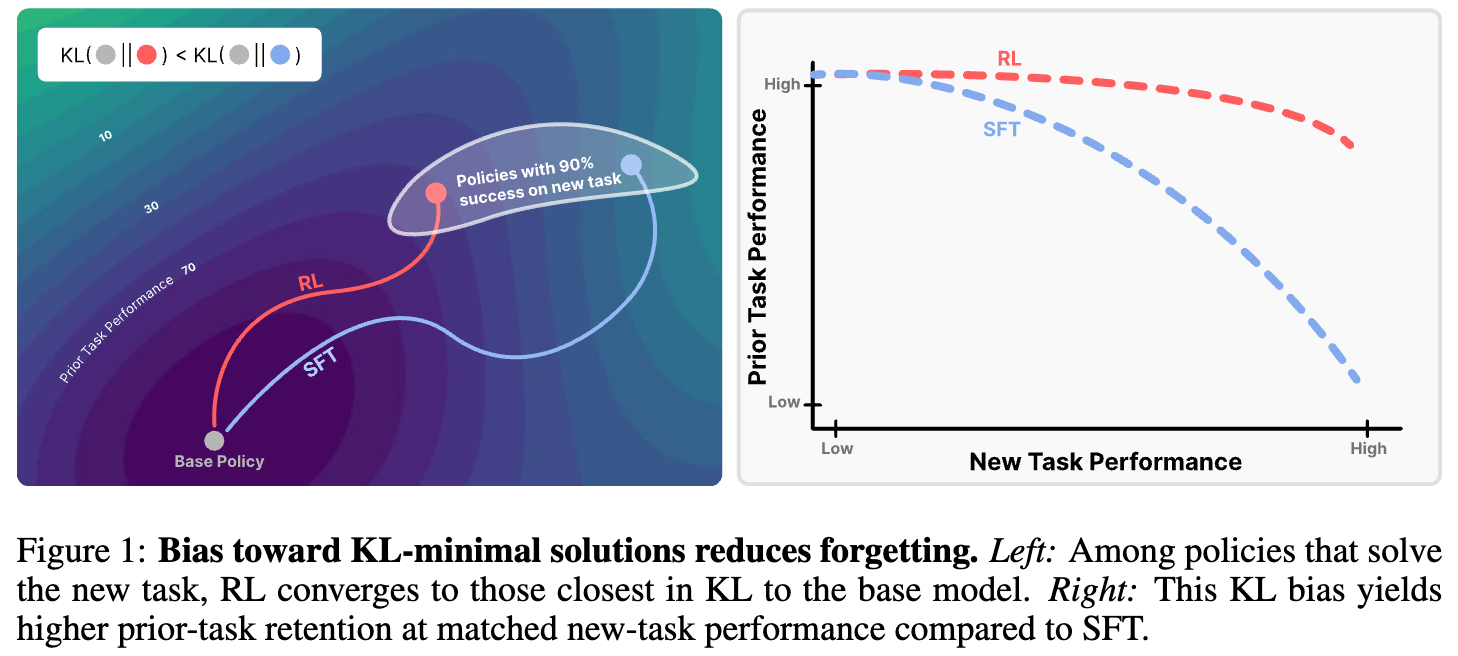
左图描绘了一个策略空间。环形区域代表那些能够在新任务上达到 90% 成功率的策略集合。基础模型（Base Policy）位于中心。当使用 SFT 进行微调时，模型可能会收敛到环上任意一点，其具体位置取决于标注数据的分布，这个解可能离基础模型非常远。相比之下，RL 微调则会收敛到环上离基础模型 KL 距离最近的那个点。

右图则展示了这种偏好所带来的实际效果。横轴是新任务的性能，纵轴是先前任务的性能（代表知识保留程度）。SFT 要想在新任务上取得高性能，必须以牺牲大量先前知识为代价。而 RL 则能在保持较高先前任务性能的同时，稳步提升在新任务上的表现。RL 的这种 KL 偏好，使其在学习-遗忘的权衡中占据了绝对优势。

总结来说，RL's Razor 提供了一个全新的视角来解释 RL 的优势：RL 的成功之处不仅在于它能有效学习新任务，更在于它在学习过程中的一种隐性的、寻求 KL 最小化的内在偏见。 接下来的部分，我们将详细探讨支撑这一论点的实验和理论证据。

实验验证：SFT 与 RL 的性能权衡

为了验证“RL 比 SFT 遗忘更少”这一核心观察，作者们进行了一系列严格的对比实验。他们选择了涵盖语言和机器人技术两大领域的多个任务，旨在检验这一现象的普适性。

实验设置

模型与任务：
- LLM, 数学推理: 使用 Qwen 2.5 3B-Instruct 模型，在 Open-Reasoner-Zero 数据集上进行数学问题求解的微调。
- LLM, 科学问答: 使用 Qwen 2.5 3B-Instruct 模型，在 SciKnowEval 数据集的化学子集上进行微调。
- LLM, 工具使用: 使用 Qwen 2.5 3B-Instruct 模型，在 ToolAlpaca 数据集上进行学习使用外部工具的微调。
- 机器人, 抓取与放置: 使用 OpenVLA-7B 视觉-语言-动作模型，在 SimplerEnv 模拟环境中进行抓取罐子的任务微调。
微调方法：
- SFT: 使用标准的监督微调方法。
- RL: 使用 GRPO（Generalized Reward Policy Optimization）算法进行强化学习微调。值得注意的是，为了公平比较，RL 训练中使用的奖励仅仅是一个二元的成功指示器（成功为1，失败为0），并且没有使用任何显式的 KL 散度正则化项。这一点非常重要，因为它表明 RL 的保守性是其算法本身内蕴的，而非外部约束的结果。
评估维度：
1. 新任务性能 (New Task Performance) ：在留存的测试集上评估模型在新学习任务上的准确率或成功率。
2. 先前任务性能 (Previous Tasks Performance) ：为了衡量遗忘程度，作者们在一系列与新任务无关的、广泛的基准测试集上评估模型。对于 LLM，这包括了 Hellaswag, TruthfulQA, MMLU 等多个知名 benchmark。对于机器人，则是在其他操作任务（如开关抽屉）上进行评估。这些任务代表了模型在微调前所具备的通用能力。

帕累托前沿分析

在比较两种算法时，简单地比较单个模型的表现是不够的，因为超参数（如学习率、批大小）的设置会极大地影响学习和遗忘之间的权衡。为了进行公平且全面的比较，作者们为每种方法都进行了广泛的超参数搜索，训练了数十个模型，并绘制了它们的帕累托前沿（Pareto Frontier）。

帕累托前沿代表了在给定方法下，所能达到的最优权衡状态。位于前沿上的任何一个点，都意味着无法在不牺牲另一个维度性能（例如，先前任务性能）的情况下，提升当前维度性能（例如，新任务性能）。

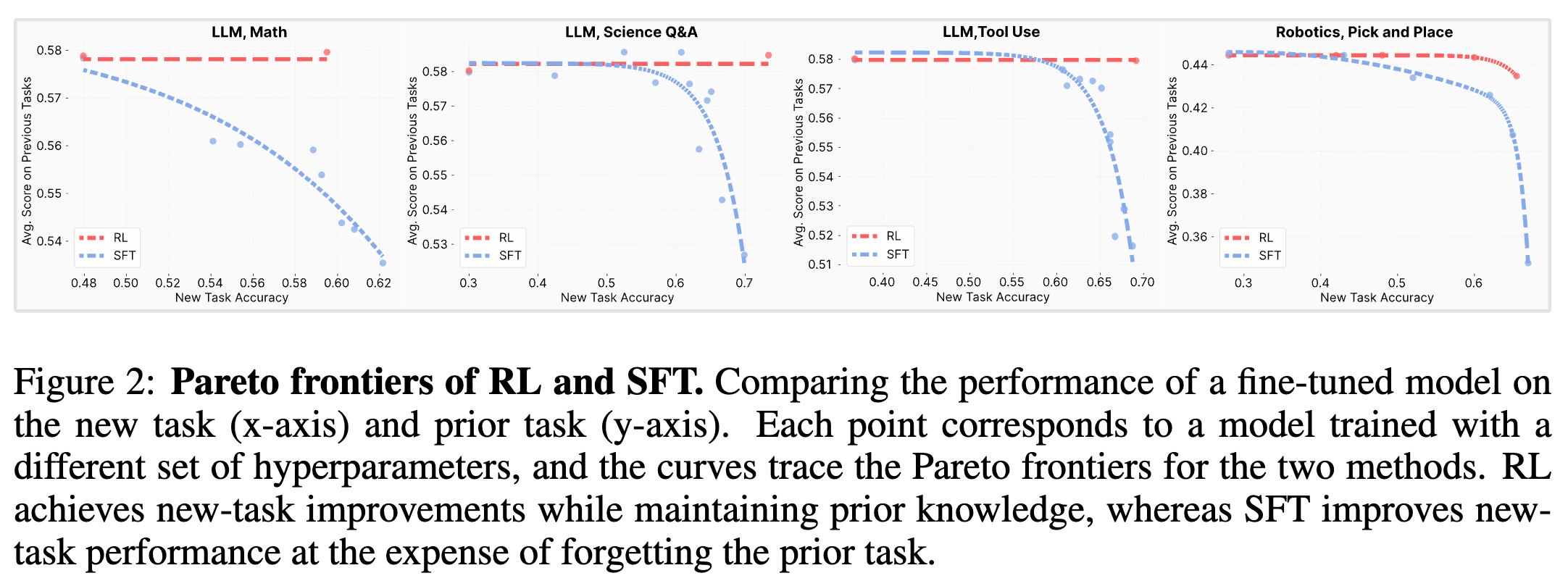
上图展示了四个任务上的实验结果。每个点代表一个经过微调的模型，曲线则连接了处于帕累托最优状态的模型。我们可以清晰地观察到一个在所有任务中都高度一致的模式：

RL 的曲线始终位于 SFT 的曲线的左上方。 这意味着，在任何给定的新任务性能水平上，RL 训练的模型都能保留更多的先前知识。
SFT 的性能权衡非常剧烈。 以数学推理任务为例，SFT 在新任务准确率上哪怕只取得微小的提升，其在先前任务上的平均得分都会急剧下降。这是一种典型的“拆东墙补西墙”的模式。
RL 则展现出更平滑、更理想的权衡。 RL 可以在显著提升新任务性能的同时，几乎不损害其在先前任务上的表现。

这些实验结果强有力地证实了论文的第一个核心观察，作者将其总结为 Takeaway 1:

RL 能够学习新任务，同时只产生微小的遗忘；而 SFT 要达到类似的新任务性能，则必须以牺牲大量先前知识为代价。

现在，我们已经确认了现象的存在。接下来，更重要的问题是：如何解释这个现象？其背后的根本原因是什么？

经验性遗忘定律 (The Empirical Forgetting Law)

在确认了 RL 和 SFT 之间的经验差距后，作者们开始探寻一个能够解释这种差异的根本性变量。一个好的解释变量应该能够独立于训练算法或超参数，统一地预测所有情况下的遗忘程度。

过去的研究提出过多种可能的解释，例如：

权重变化的大小: 限制模型参数的变化幅度。
梯度的稀疏性或秩: 认为 RL 的梯度更新更稀疏。
表征的变化: 保持模型内部隐藏层表示的稳定。

然而，作者们通过实验发现，这些变量都不能与观测到的遗忘现象形成稳定、一致的关联。在不断探索中，发现了一个出乎意料但异常稳健的规律，并将其称为“经验性遗忘定律” (Empirical Forgetting Law) 。

经验性遗忘定律

这一定律指出：

在对一个模型进行微调以适应新任务时，其遗忘的程度可以被一个指标精确地预测：在新任务的数据分布上，微调后的策略与基础策略之间的前向 KL 散度，即。

这个定律的非凡之处在于它的简洁性和实用性。它告诉我们，遗忘的程度本质上是由模型在新任务上其输出分布偏离原始分布的程度决定的。这个偏离可以用 KL 散度来量化。更重要的是，这个指标可以在微调过程中进行监控和度量，因为它只需要访问基础模型和新任务的数据，而不需要访问庞大甚至未知的先前任务数据。

在受控环境 (ParityMNIST) 中验证定律

由于在大型模型上进行细致的变量剥离和假设检验计算成本极高且难以控制，作者们设计了一个巧妙的“玩具”实验环境——ParityMNIST——来精确地验证上述定律。

实验设置:
- 他们构建了一个简单的 3 层 MLP 网络。
- 预训练阶段：在 ParityMNIST（判断 MNIST 手写数字是奇数还是偶数）和 FashionMNIST（一个标准的图像分类任务）的混合数据上进行联合预训练。
- 微调阶段：只在 ParityMNIST 任务上进行微调。
- 遗忘衡量：在 FashionMNIST 任务上评估性能下降程度。

这个设置的精妙之处在于，ParityMNIST 任务具有“多解性”（many valid solutions）。例如，对于一个偶数图片“2”，模型可以预测为“0”、“2”、“4”、“6”或“8”中的任何一个，或者它们的任意概率组合，只要它不把概率分配给奇数即可。这与 LLM 的生成任务非常相似，即一个 prompt 可以有多个正确的续写。这种多解性为检验不同算法的偏好提供了理想的温床。

实验结果:

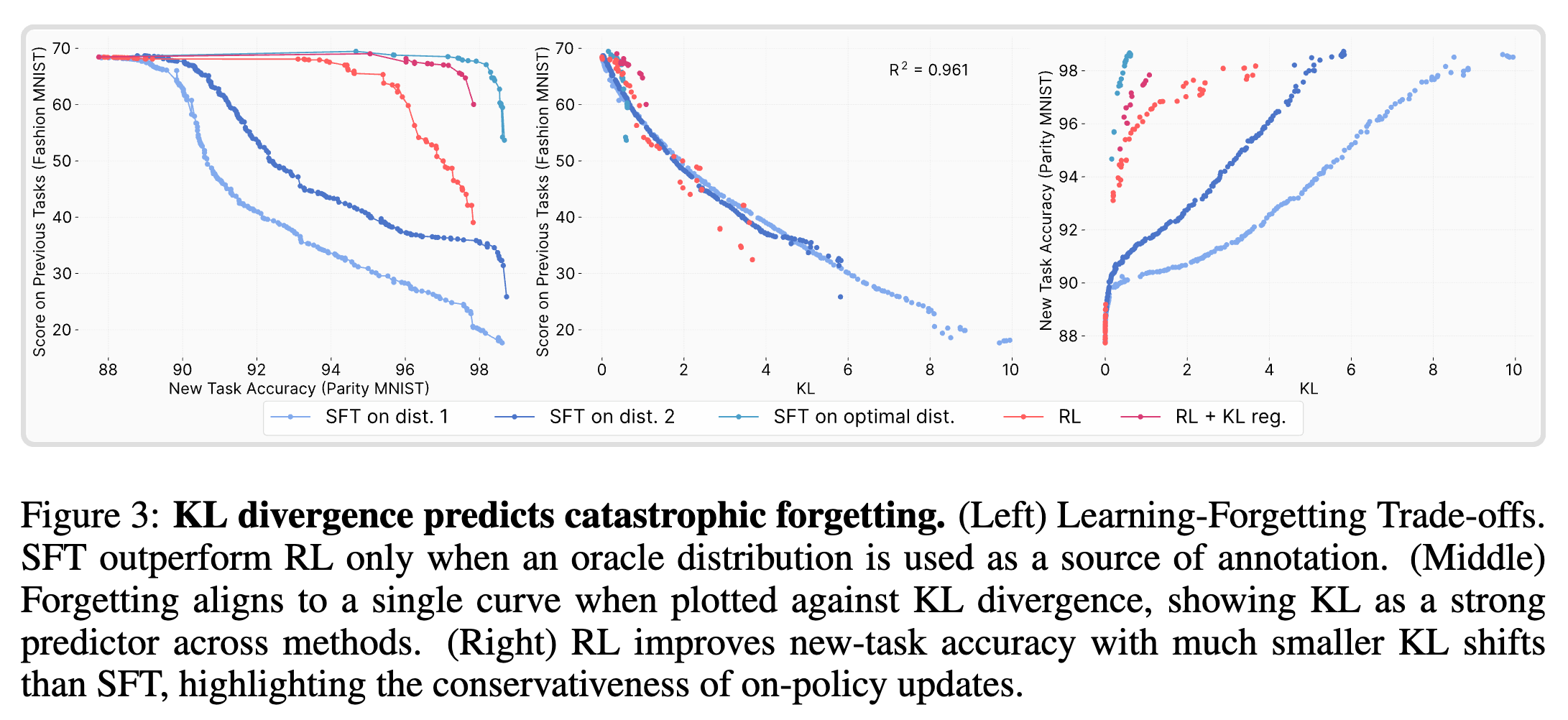
上图展示了 ParityMNIST 实验的关键结果，它分为三个部分：

左图 (Learning-Forgetting Trade-offs): 这个图成功地复现了在大型模型上观察到的现象。RL 的学习-遗忘权衡曲线优于标准的 SFT。这证明了 RL 的优势并非 Transformer 架构所特有，而是一个更普遍的现象。
中图 (Forgetting aligns to a single curve when plotted against KL divergence): 这是验证“经验性遗忘定律”的核心证据。 作者将所有实验（包括不同超参数下的 RL 和 SFT）的遗忘程度（纵轴）与它们各自的 KL 散度（横轴）绘制在一起。惊人的是，所有的点几乎完美地落在了同一条二次曲线上（）。这表明，决定遗忘的直接因素就是 KL 散度，而不是你使用的是 RL 还是 SFT 算法。无论你走哪条路，只要你离起点的 KL 距离是 X，你遭受的遗忘就是 Y。
右图 (RL improves new-task accuracy with much smaller KL shifts): 这张图解释了为什么 RL 的权衡曲线更优。它显示，为了达到相同的新任务准确率，RL 所产生的 KL 散度位移远小于 SFT。RL 找到了一条“捷径”，用更小的分布变化就解决了新问题。

Oracle SFT 的思想实验

为了进一步确认 KL 散度是决定性变量，作者们进行了一个思想实验。如果 KL 散度真的是遗忘的“总开关”，那么我们是否可以构造一个“最优”的 SFT，使其遗忘程度比 RL 还小？

答案是肯定的。在 ParityMNIST 这个简单的环境中，作者们可以解析地计算出一种 SFT 标注分布，这种分布在确保 100% 正确率的前提下，与基础模型的 KL 散度是最小的。他们称之为“神谕 SFT 分布” (Oracle SFT Distribution) 。

实验结果如左图曲线所示，使用这个神谕分布训练的 SFT 模型，其学习-遗忘权衡曲线甚至超越了 RL。这雄辩地证明了，RL 的优势并非源于其算法本身的某种魔力，而是源于其隐性的 KL 最小化偏见。 当 SFT 被显式地引导去最小化 KL 散度时，它也可以取得同样甚至更好的效果。

此外，他们还做了一个“蒸馏”实验：用一个 RL 训练好的模型来生成数据，然后再用这些数据去训练一个 SFT 模型。结果发现，这个被“蒸馏”的 SFT 模型的性能曲线与 RL 的曲线几乎完全重合。

这些实验共同指向了论文的第二个核心结论，Takeaway 2:

无论是 SFT 还是 RL，灾难性遗忘的程度都由微调后的模型与基础模型在新任务上的 KL 散度所决定。

至此，我们已经将问题从“为什么 RL 遗忘更少”转化为“为什么 RL 能够以更小的 KL 散度解决新任务”。

理论解释：为何在线策略 (On-Policy) 能最小化 KL 散度

现在，我们来解答最后一个，也是最根本的问题：为什么 RL 微调天然地就能找到那些 KL 散度更小的解？

作者们认为，关键在于 RL 的在线策略（On-policy）特性。为了理解这一点，我们首先需要对比 SFT 和 RL 的优化目标。

SFT 的目标函数:

在 SFT 中，模型的目标是最大化在给定数据集上的对数似然。这个数据集中的标签来自一个固定的、外部的监督分布（例如，人类标注员给出的答案）。优化过程就像是把模型的分布 “拽”向目标分布，而可能与模型的初始分布相距甚远。
RL (策略梯度) 的目标函数:

在 RL 中，特别是基于策略梯度的方法，优化的期望是基于模型自身的输出分布 来计算的。是优势函数（Advantage function），代表了采取行动所获得的回报相对于平均回报的好坏。RL 的学习过程是：模型自己先生成一个输出，然后环境（或奖励模型）给这个打分，模型根据分数来调整下一次生成这个的概率。

两个关键区别：采样分布与负样本

从目标函数可以看出，RL 和 SFT 至少存在两个显著差异：

采样分布 (Sampling Distribution): RL 是在线策略的，它从自己当前的策略分布中采样数据进行学习。而 SFT 是离线 (Offline) 的，它使用一个预先收集好的、固定的数据集。
负样本 (Negative Examples): RL 在探索过程中会生成各种各样的输出，其中既有好的（高回报），也有不好的（低回报，即负样本）。它能从这些负样本中学习，明确地降低坏输出的概率。而标准的 SFT 数据集通常只包含“正确答案”，缺乏对负样本的学习。

那么，究竟是哪个因素导致了 RL 的 KL 保守性呢？是“在线策略”的特性，还是“学习负样本”的能力？

消融实验

为了解耦这两个因素，作者们设计了包含四种算法的对比实验：

GRPO: 在线策略 + 利用负样本 (标准的 RL)。
1-0 Reinforce: 在线策略 + 不利用负样本 (只对奖励为 1 的“正确”样本进行梯度更新，忽略奖励为 0 的样本)。
SFT: 离线策略 + 不利用负样本。
SimPO: 离线策略 + 利用负样本 (一种能够利用正负样本对的离线优化算法)。

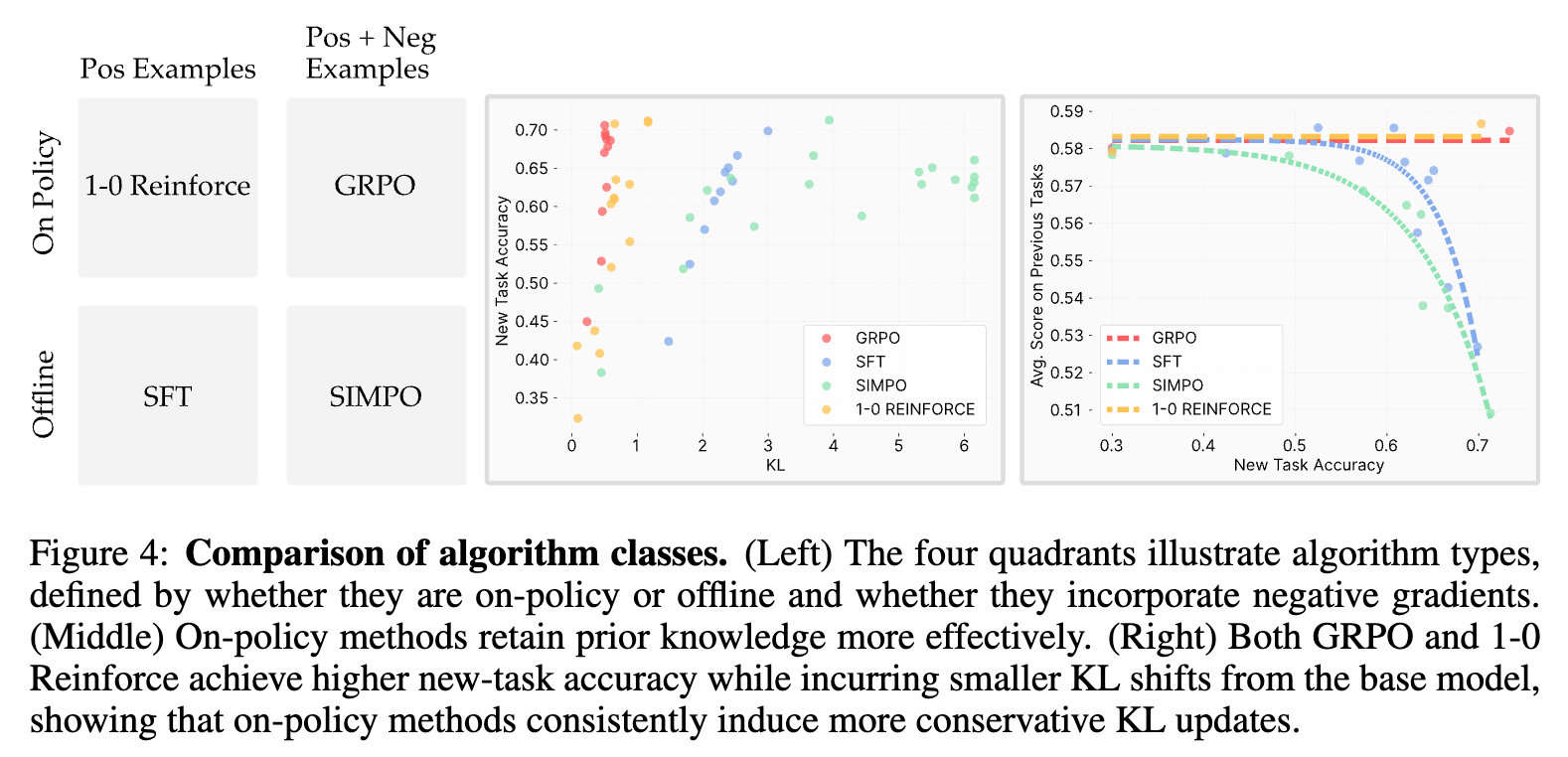
实验结果（如上图右侧所示）非常清晰：

GRPO 和 1-0 Reinforce 的表现非常相似，它们都以较小的 KL 散度代价实现了较高的任务性能。
SFT 和 SimPO 的表现也非常相似，它们都需要付出巨大的 KL 散度代价。
两条界线泾渭分明，正好划分在“在线策略”和“离线策略”之间。

这个实验有力地证明了，“在线策略”的采样机制是决定性因素，而是否利用负样本则关系不大。

理论视角

为什么在线策略采样会自然地导致更小的 KL 变化？从理论上讲，策略梯度方法可以被看作是一种在概率空间中的保守投影。

直观地理解：

每一步更新时，RL 都是基于当前模型认为比较可能的输出来进行调整。它会对这些输出根据奖励进行“重新加权”，略微增加好输出的概率，降低坏输出的概率。整个过程是渐进式的，像是“小步快跑”，始终围绕着模型当前的分布进行微调。
相比之下，SFT 的目标是远方的一个固定靶心（监督数据的分布）。如果这个靶心离模型当前位置很远，SFT 的梯度会直接将模型向那个方向猛拉，导致剧烈的分布变化。

作者们进一步从数学上 formalize 了这个观点。他们证明了，在二元奖励（0或1）的简化设定下，策略梯度算法的每一步更新，等价于一个两阶段的交替投影过程，这个过程在数学上被称为 EM 算法与信息投影 (EM with information projection) ：

I-Projection (信息投影): 将当前策略投影到所有最优策略（即奖励为1的策略）的集合中，找到 KL 散度最小的那个策略。这一步对应于 RL 中的“采样并根据奖励进行筛选”。
M-Projection (矩投影): 将上一步得到的中间策略投影回模型能表示的策略空间中，找到 KL 散度最小的新策略。这一步对应于策略参数的梯度更新。

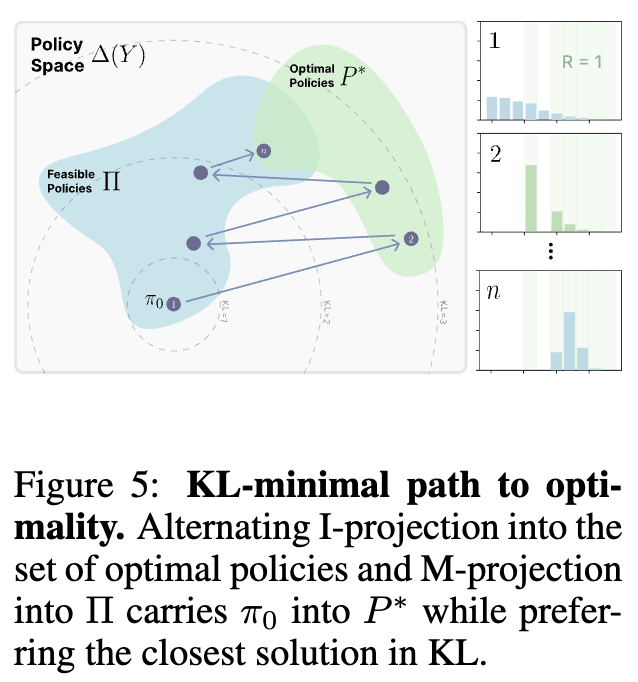
上图直观地展示了这个交替投影的过程。它描绘了在策略空间中，初始策略如何通过一系列交替的 I-投影（投影到最优策略集）和 M-投影（投影回模型可表示的策略集），最终收敛到那个在中、同时离最近的解。

这套理论（Theorem 5.2）优美地证明了：

在适当的条件下，策略梯度方法会收敛到那个在所有可实现的最优策略中，与初始策略的 KL 散度最小的那个解。

这个理论为 RL's Razor 提供了坚实的数学基础。它揭示了，即使没有在目标函数中加入显式的 KL 正则项，在线策略的 RL 算法本身就在进行着一场隐式的 KL 最小化优化。

这便是论文的第三个，也是最深刻的结论，Takeaway 3:

在线策略训练解释了为何 RL 能保持较小的 KL 散度。从模型自身分布中采样使其与基础模型保持紧密，而 SFT 则将模型推向一个任意的外部数据分布。

排除其他假设

为了使论证更加严谨，作者们还系统性地评估了其他一系列可能解释遗忘现象的替代理论，并将它们与前向 KL 散度（Forward KL）的预测能力进行了定量比较。

他们在 ParityMNIST 任务上计算了各种指标与遗忘程度之间的相关性系数（通过二次多项式拟合）。

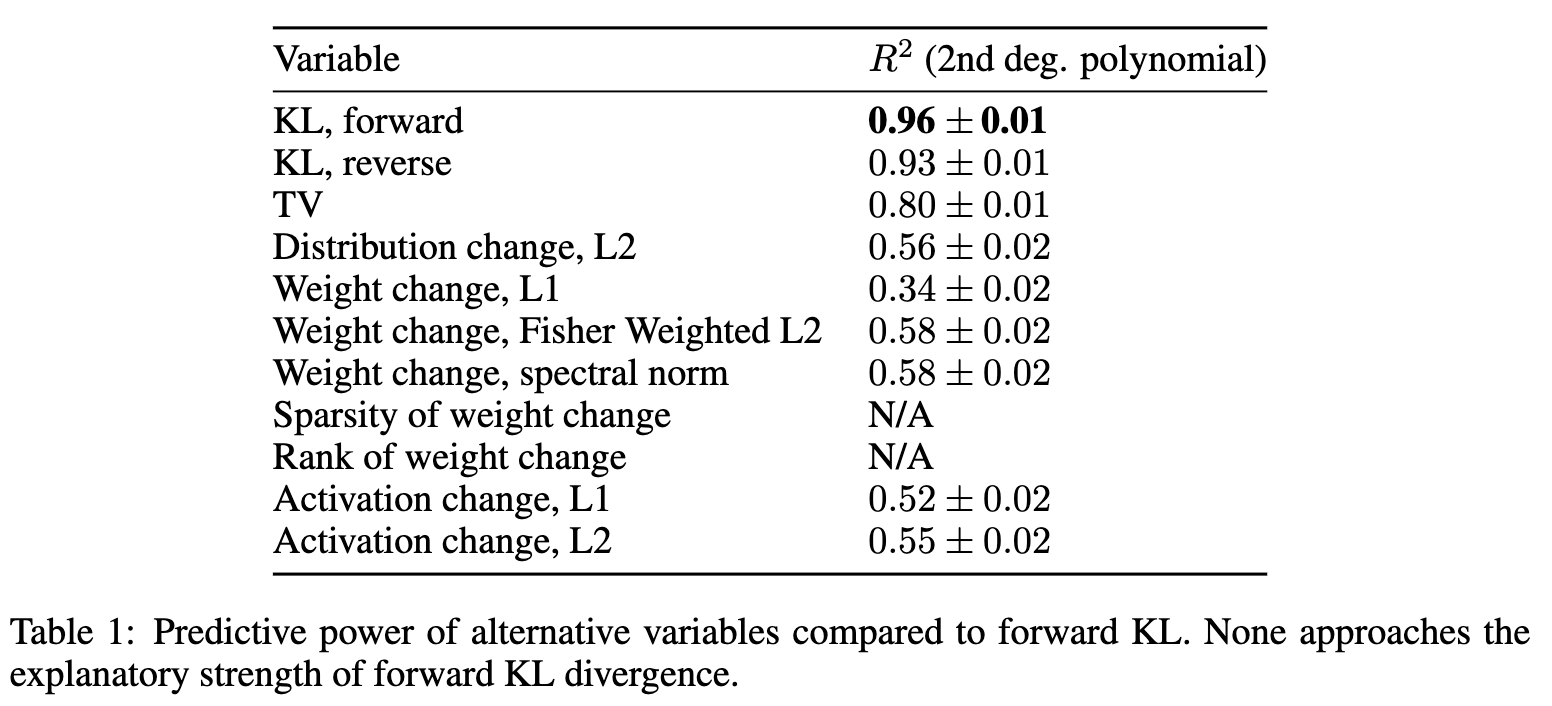
从上表中可以清晰地看到：

前向 KL 散度 (KL, forward) 的预测能力一骑绝尘，其值达到了。
反向 KL 散度 (KL, reverse) 也表现出较强的信号（），但仍不及前向 KL。
其他基于分布变化的度量，如总变差（TV）和 L2 距离，相关性要弱得多。
而那些基于权重变化（Weight change）或表征变化（Activation change）的传统指标，其预测能力都非常有限（值普遍在 0.3-0.6 之间），与遗忘没有稳定的函数关系。

这一系列的排除性实验，进一步巩固了 KL 散度作为预测灾难性遗忘的核心指标的地位，也让 RL's Razor 的解释框架更加令人信服。

总结

RL 能够学习新任务，同时只产生微小的遗忘；而 SFT 要达到类似的新任务性能，则必须以牺牲大量先前知识为代价。
无论是 SFT 还是 RL，灾难性遗忘的程度都由微调后的模型与基础模型在新任务上的 KL 散度所决定。
在线策略 (On-Policy) 能最小化 KL 散度。

往期文章：

一	二	三	四	五	六	日
1	2	3	4	5	6	7
8	9	10	11	12	13	14
15	16	17	18	19	20	21
22	23	24	25	26	27	28
29	30