近期，扩散语言模型（Diffusion Language Models, DLMs）的研究热潮凸显了其巨大的潜力。得益于并行的解码设计，DLMs 能够以每秒数千个词元（token）的速度生成文本，为实际应用带来了极低的延迟 [17, 18, 19]。此外，一些最新的 DLMs 在性能上已经可以与自回归（Autoregressive, AR）模型相媲美 [8, 9]。

但速度是它们唯一的优势吗？经过过去数月严谨的探索，我们揭示了一个更引人注目的特性：在固定的数据预算下，扩散模型是卓越的数据学习者。 这意味着，在给定相同数量的唯一预训练词元（unique pre-training tokens）的情况下，通过投入更多的浮点运算（FLOPs）来换取更优的学习效果，扩散模型的性能始终优于同等规模的自回归模型。这反映出其数据潜力大约是 AR 模型的三倍以上。

随着我们逐渐逼近可用预训练数据的上限 [20]，这种数据潜力变得日益珍贵，尤其是考虑到 AR 模型在数据重用四轮（epochs）后便显示出收益递减的现象 [11]。巧合的是，一篇同期的研究《Diffusion Beats Autoregressive in Data-Constrained Settings.》[1] 也探讨了类似的主题。然而，我们经过审慎分析，发现该研究 [1] 中存在若干方法论上的问题，可能导致其结论存在偏差。

在这篇博客中，我们将首先展示初步的实验结果，这些结果为扩散模型在特定“交叉点”超越 AR 模型提供了强有力的证据。随后，我们将深入剖析扩散模型的学习行为，以揭示其优势的来源。最后，我们将详细评析研究 [1] 中存在问题的方法论，旨在为未来更稳健的研究指明方向。

文章亮点

• 我们从零开始预训练了参数量高达 80亿（8B）、处理词元总量达 4800亿（480B） 的 DLMs 和 AR 模型。结果表明，DLMs 相较于 AR 模型展现出超过 3倍 的数据潜力。值得注意的是，一个 10亿参数的掩码扩散模型，仅仅通过重复使用标准的10亿词元预训练数据，就在 HellaSwag 测试上取得了超过 56% 的准确率，在 MMLU 上超过 33%，且未采用任何特殊技巧。由于未观察到收益递减的迹象，更多的重复训练有望进一步提升其性能。
• DLMs 是“超级密集”型模型，其消耗的 FLOPs 远超于密集的 AR 模型。为了充分利用数据，训练 DLMs 通常需要至少两个数量级的额外 FLOPs。在推理阶段，生成长度从16到4096个词元的序列，其 FLOPs 开销相比 AR 基线模型增加了 16倍到4700倍。此外，扩散目标函数所支持的表现力更强的双向注意力机制，使得模型能够双向地对语言数据进行建模。现实世界的文本数据并非完全遵循因果顺序，这种双向建模能力能够更充分地挖掘数据价值。
• 我们的同期工作《数据受限下，扩散模型击败自回归模型》中存在一些方法论问题，可能导致结论出现偏差，这些问题包括：有问题的扩散损失函数公式、无效的比较指标、对 AR 模型不公平的实验设置，以及有问题的缩放定律（scaling law）公式。这些问题都可能导致潜在的误导性结果和结论。

1. 初步实验结果

✨ 本节亮点

1. 我们从零开始训练了高达 80亿参数和 4800亿词元的 DLMs 和 AR 模型。在唯一数据受限的情况下，通过重复数据，DLM 在某个点上明显超越了 AR 对手，展示了比 AR 模型高出3倍以上的数据潜力。值得注意的是，不同评估基准上的交叉点是相似的。
2. 一个10亿参数的掩码扩散模型，仅通过重复标准的10亿词元预训练数据，就在 HellaSwag 上达到了 >56% 的准确率，在 MMLU 上达到了 >33%，无需任何特殊技巧。由于未观察到收益递减，更多的重复训练可能进一步提升其性能。
3. 在验证集上“过拟合”的模型，在下游任务上的表现往往会持续提升。 过拟合后，绝对负对数似然（NLL）因模型的过度自信而上升，但 △NLL（正确答案与错误答案NLL的差距）持续扩大，表明其判别能力得以保持甚至增强。
4. 尽管对数据重复具有鲁棒性，DLMs 也会过拟合——只要我们训练足够多的轮次。更大的唯一数据量可以推迟过拟合的发生，而更大的模型则会加速其到来。

1.1 智能交叉点 (The Intelligence Crossover)

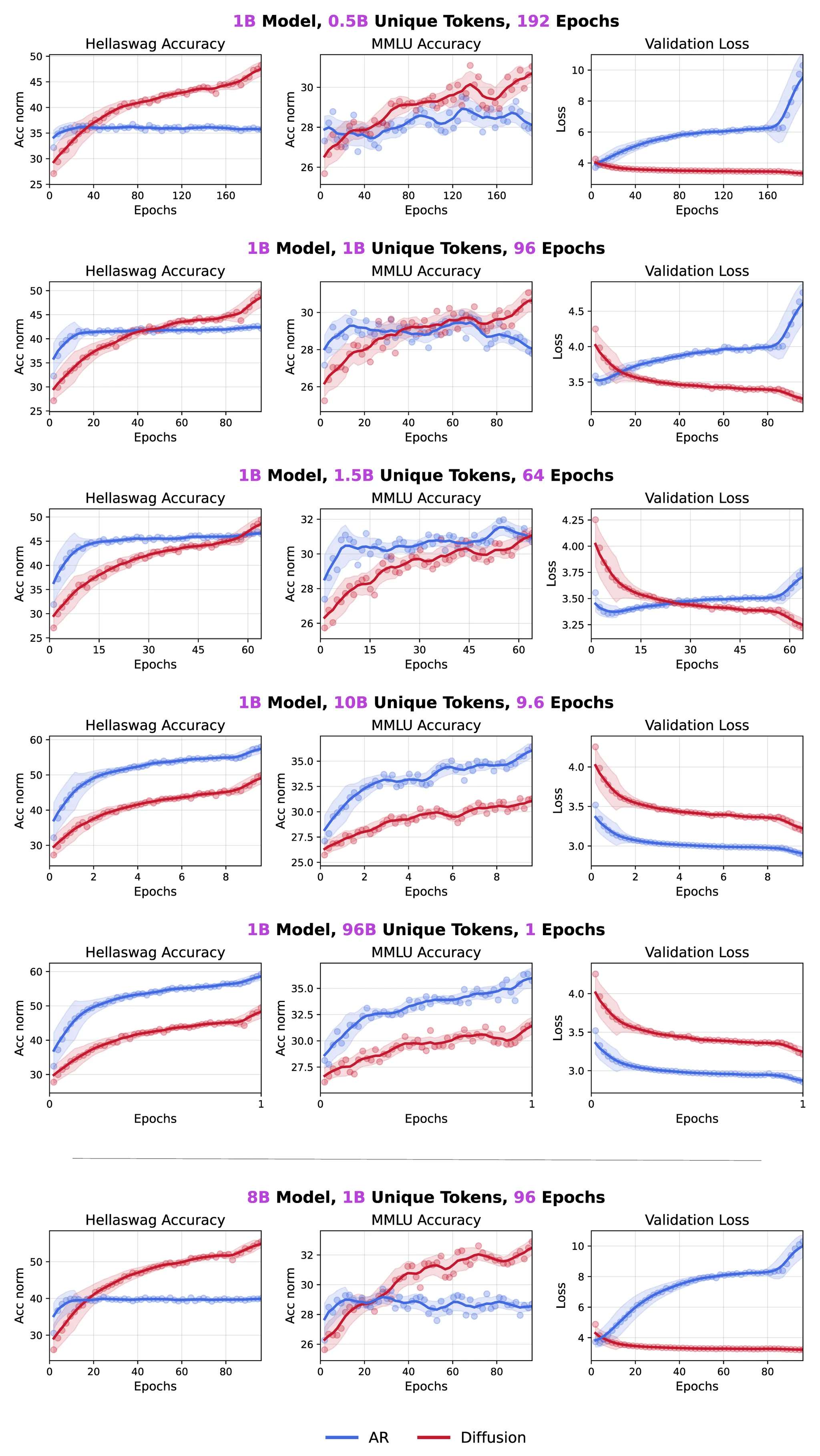
整体设置： 密集的10亿/80亿参数模型在一个固定的960亿词元预算上进行训练，唯一词元数从5亿到960亿不等。一个10亿参数的 DLM 还在10亿唯一词元上训练了480个轮次。

图 A 展示了一系列广泛的实验结果，提供了令人信服的证据：通过在普通网络数据上进行重复训练，在数据受限的情况下，无论模型规模大小，掩码 DLMs 的性能都优于 AR 对手，并展现出显著更强的数据潜力，且未出现性能饱和。

总体而言，我们的结果表明 DLMs 展现出超过三倍于 AR 模型的最终数据潜力。这一估计在我们的实验中得到了经验支持，因为仅在5亿唯一词元上训练的 DLMs（未收敛）的性能，已经可以与在15亿唯一词元上训练的 AR 模型（已收敛）相媲美。将模型规模从10亿参数增加到80亿，进一步释放了数据潜力，而 AR 模型在数据受限的情况下，并不能从更大的模型规模中获益。当唯一数据从960亿词元急剧减少到5亿时，DLMs 的性能下降也微不足道。

在计算受限（compute-bound）的场景下——即数据供应充足——AR 模型能更好地拟合训练数据，因此在训练结束时能取得更优的性能。然而，在数据受限（data-bound）的条件下——这反映了当前计算能力增长速度超过数据可用性的现实——扩散模型在某个点上显著超越了 AR 模型。关于这一现象的更深入分析将在第二部分呈现。

值得注意的是，在不同评估基准上观察到的交叉点是相似的（本例中仅使用了两个通用领域的评估）。当我们增加唯一词元的数量时，DLMs 超越 AR 模型的交叉点会向后推迟（如在0.5-1.5B唯一词元区间所见），甚至可能移出我们的可观察范围（1.5-96B区间）。这种推迟现象在1.3节中观察得更为清晰。100亿和960亿唯一词元运行之间的差距较小，是因为交叉点被大幅推迟，我们在0-96B词元窗口内观察到的只是一个初始模式，而初始阶段的差异通常弱于后期。

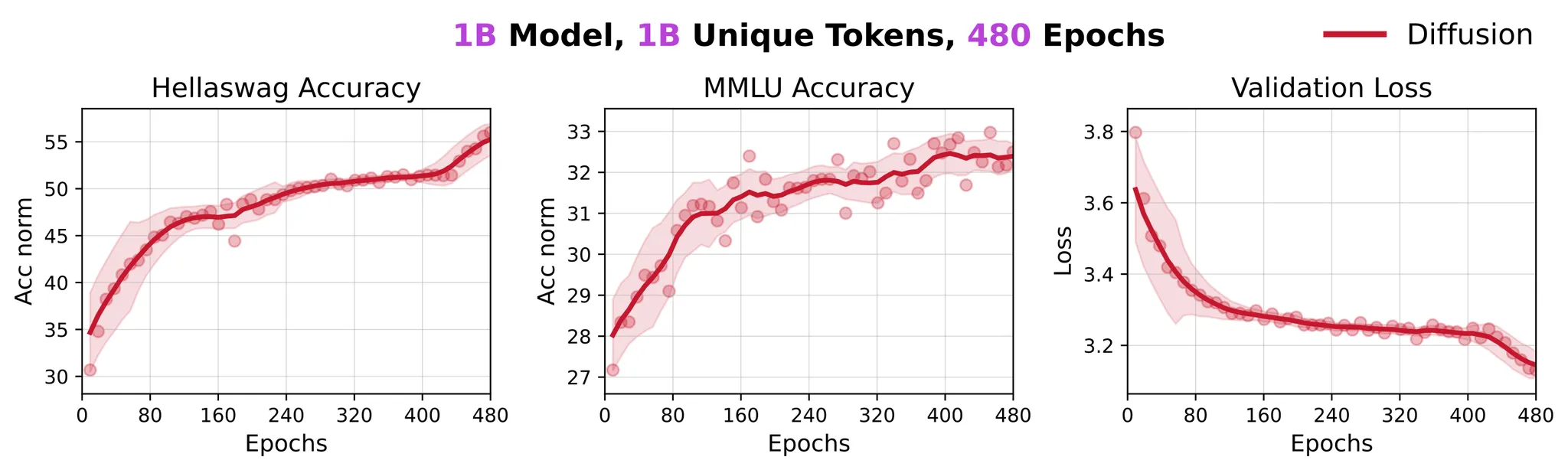
为了研究词元在 DLM 训练中的全部潜力，我们进行了一项额外的实验，将同一个10亿词元的数据集重复训练了480个轮次，总训练词元达到4800亿。值得注意的是，该模型在 HellaSwag 上取得了约56%的准确率，在 MMLU 上取得了约33%的准确率，显著优于 AR 模型约41%和29%的相应表现。令人惊讶的是，即使在如此极端的数据重复下，模型性能也并未饱和，这表明 DLMs 能够从一个固定的10亿词元语料库中提取出远为丰富的信号。

1.2 高验证损失 ≠ 智能退化

在本节中，我们将论证为什么在比较扩散模型和 AR 模型时，下游任务的评估结果比验证损失更为关键，以及为什么我们需要呈现覆盖整个观察范围的大量基准数据点，而不是仅仅展示单个数据点。

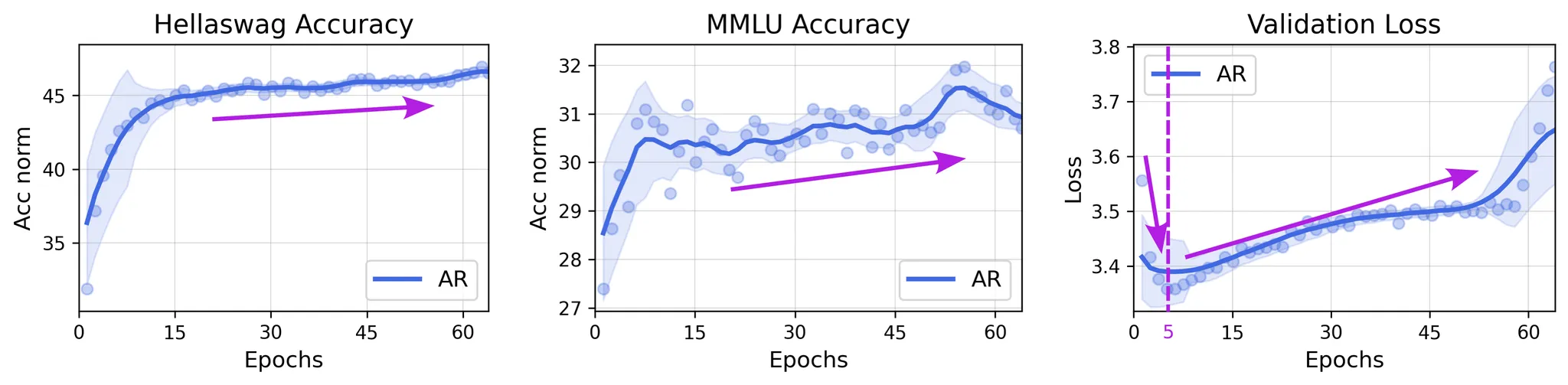
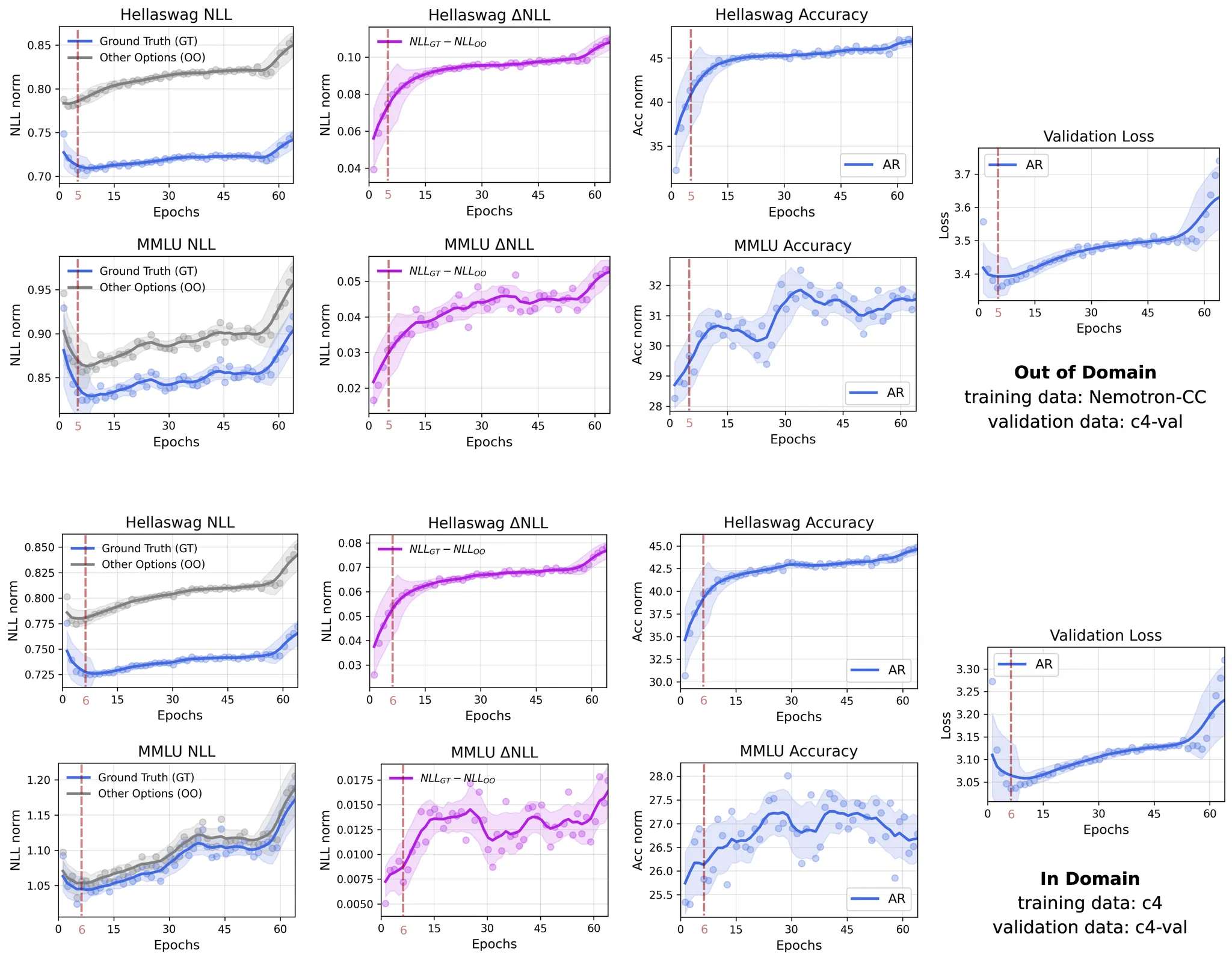
在图 D 中，我们可视化了一个10亿参数的 AR 模型在15亿唯一词元上训练64个轮次期间，多项选择评估中正确答案和错误选项的平均负对数似然（NLL）及其差异（△NLL）。值得注意的是，即使在第一个验证点（训练3600步后），模型已经对正确答案表现出显著更低的 NLL（即更高的似然），这表明模型很早就具备了为正确选项赋予更高 logits 的能力。随着训练的继续，模型开始过拟合，导致正确和错误选项的 NLL 值双双上升。有趣的是，即使在这种“过拟合”之后，正确答案与错误选项 NLL 之间的差距仍然持续稳定地扩大，这表明尽管验证损失在上升，但模型底层的判别能力仍在不断提高。 这一现象在领域内和领域外的训练数据上都同样存在。

一种合理的解释是，反复接触有限的训练数据使模型对某些文本片段变得过度自信，从而放大了对错误预测的 NLL 值。然而，正确选项与其他选项之间相对 NLL 差异的持续增长，反映了模型判别能力的不断提升。类似的逻辑也适用于生成式评估，其中选择是在词元级别而非句子级别进行的。我们假设，对非关键性词元的错误过度自信对整体任务的影响有限。这一假设将在我们即将进行的、使用更大规模模型和更大唯一数据集的研究中进一步验证，因为在小计算预算下训练的模型通常难以在基于生成的评估中展现出平滑的趋势。

1.3 扩散语言模型同样会过拟合

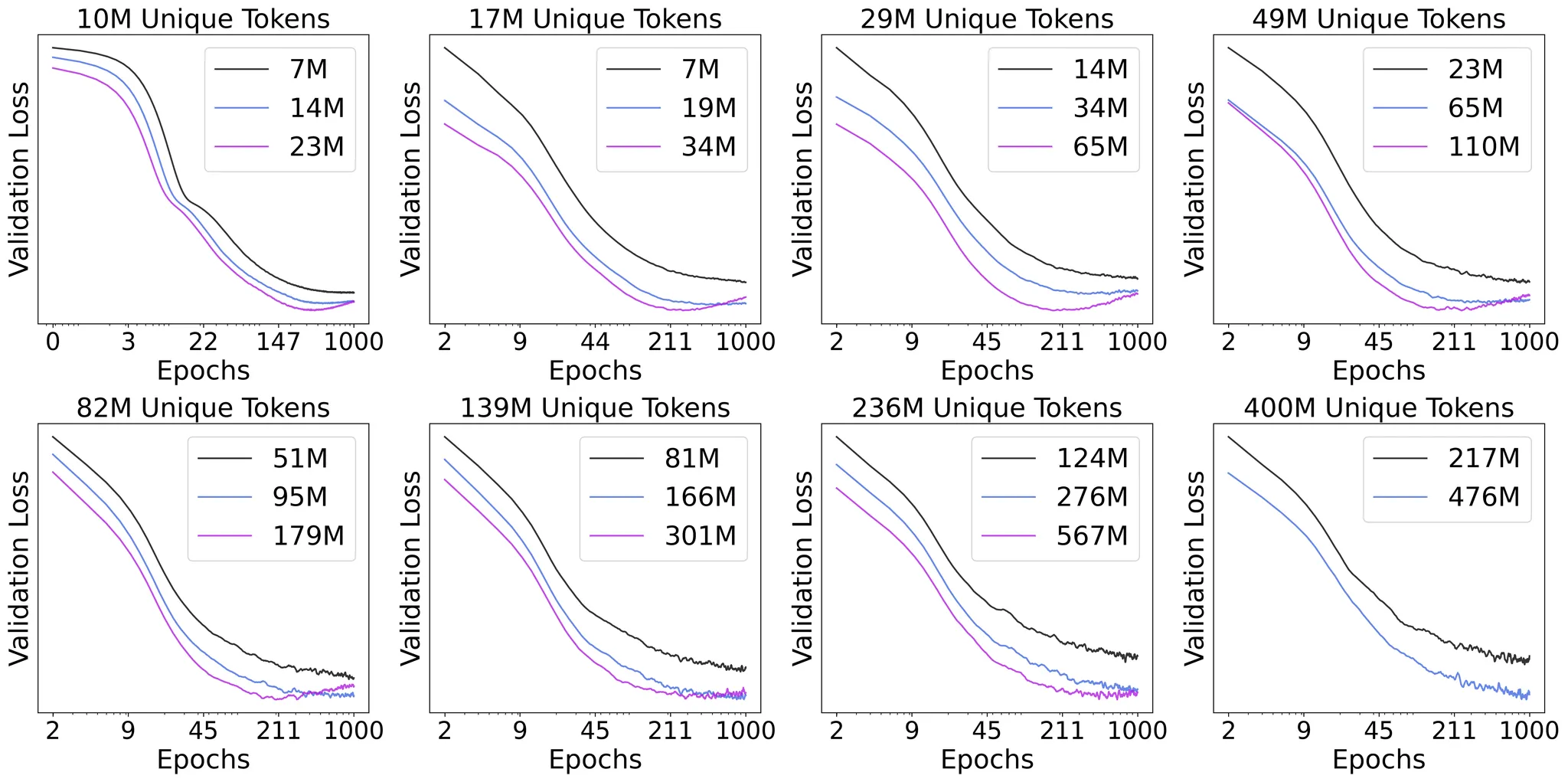
在图 A 中，当我们在极度有限的唯一数据（低至5亿词元）上进行大量轮次（高达480轮）的训练时，我们并未观察到 DLMs 的收益递减，更不用说过拟合了。这引导我们去探究：如果给予足够长的训练，DLMs 最终会过拟合吗？

我们训练了不同规模和不同唯一数据预算的模型，并将训练延长至1000个轮次。如图 E 所示，当唯一数据足够少且模型规模足够大时，在长时间的训练后，过拟合最终还是会出现。

具体来说，我们观察到模型开始过拟合的轮次与唯一数据量呈正相关，与模型规模呈负相关。换言之，更大的唯一数据量会推迟过拟合的发生，而更大的模型则会加速其到来。

需要重点指出的是，验证损失的过拟合并不立即意味着模型能力的下降——实际性能的退化通常发生在更晚的时候（例如，如图 A 所示，在5亿词元和192轮次时）。我们将在论文的完整版本中详细讨论这种智能退化的确切时机。

关键实验设置

值得一提的是，我们实验中采用的超参数主要针对 AR 模型进行了优化，这反映了更广泛的 LLM 研究社区长期以来的大量调优工作。尽管我们试图在 AR 和扩散模型之间保持设置一致，但这对于扩散模型而言本身就是不公平的。因此，我们观察到的扩散模型的性能优势可能被低估了。

所有训练运行都使用了经过显著修改的 Megatron-LM 代码库。交叉点实验在 Nemotron-CC 语料库 [2] 的一个子集上进行，而所有其他实验则使用了 c4-en 语料库 [3] 的一个子集。请注意，所有使用的词元预算都是从这些语料库中随机抽样的，没有任何特殊处理。 我们使用了与 [8] 中相同的掩码扩散目标函数，具体细节在公式2中详述。具体而言，我们采用了256的批量大小、2048的序列长度，以及一个峰值为2e-4的“预热-稳定-衰减”（WSD）学习率调度，其中预热步骤为1000步，随后以10%的指数衰减至2e-5。模型参数从标准差为0.02的正态分布中随机初始化。我们采用了一种高性能的架构配置，包括 GPT-2 分词器、RoPE、SwiGLU、前置层 RMSNorm、无偏置和 qk 归一化。验证损失在 c4-en 验证集上评估，每次评估使用不同的1亿词元子集，并且基准评估严格遵守官方协议。

2. 扩散语言模型是超级数据学习者

敬告： 本节主要基于一些证据进行理论分析，未经审慎的消融实验。

✨ 本节亮点

1. DLMs 是超级数据学习者，因为 (1) 它们的双向建模能力，得益于扩散目标和双向注意力，能更彻底地挖掘并非完全因果的网络数据；(2) 它们的计算超级密度——即每个任务投入更多 FLOPs——直接转化为更强的智能。
2. AR 模型优先考虑计算效率而非数据利用率。 它们的 Transformer 设计——采用教师强制（teacher forcing）和因果掩码（causal masking）——最大化了 GPU 利用率，但限制了建模能力。随着计算成本变得越来越低，数据可用性成为关键瓶颈——这正是我们研究 DLMs 的动机。
3. 扩散目标明确要求预训练数据集中的每个数据点在多种掩码率和组合下被破坏，以便进行有效训练，这为数据重复为何能带来如此巨大的增益提供了另一个视角。

2.1 扩散语言模型的真正优势是什么？

文献 [1] 在其摘要中进行了如下讨论：

“我们将这种优势解释为隐式的数据增强：掩码扩散使模型暴露于多样化的词元排序和预测任务中，这与 AR 模型固定的从左到右的分解方式不同。”

“数据增强”的观点可能并未触及核心。向数据中注入噪声确实是提升模型泛化能力的一种方式，在视觉领域相当普遍，但这并非颠覆性的改变——你也可以向 AR 模型中注入噪声，但这并不会带来实际的增益 [21]。

相反，真正的优势在于，扩散目标函数解锁了一种使用表现力更强的双向注意力来双向建模真实世界数据的方式。这一优势是颠覆性的，并带来了两大直接好处：

• 通过双向建模减少归纳偏置 (Inductive Bias)。 自回归语言模型对文本数据建模施加了严格的因果归纳偏置，即每个词元的预测仅依赖于其前面的词元。虽然从人类视角看，自然语言具有内在的因果性，但有证据表明，以反向或任意顺序对语言进行建模仍然是可行的 [12]。此外，许多非因果类型的数据，如源代码、数据库条目、符号表示法和生物序列等，也频繁出现在网络上。因此，强制采用纯粹的因果归纳偏置，极大地限制了模型捕捉多样化文本分布中丰富模式的能力。DLMs 通过一个支持双向建模的目标函数消除了这种归纳偏置，从而能够充分挖掘每个数据点的价值。
• 超级密度：训练和测试时每个任务投入更多的 FLOPs。 如图 F 所示，扩散模型通过在训练期间重复处理一部分唯一数据，有效地在时间维度上扩展了 FLOPs，从而超越了自回归模型。掩码语言模型所使用的连续时间目标函数尤其有利，它支持了时间维度上 FLOPs 扩展的高粒度性。同样，在推理时，扩散模型通过迭代地精炼预测，进一步放大了每个任务的计算密度。值得注意的是，双向注意力意味着生成一个长度为 N 的序列时，每个词元最多被计算 N 次，这与使用 KV 缓存、每个词元只计算一次的自回归模型形成鲜明对比。

对训练和推理 FLOPs 的比较分析 (图 F)

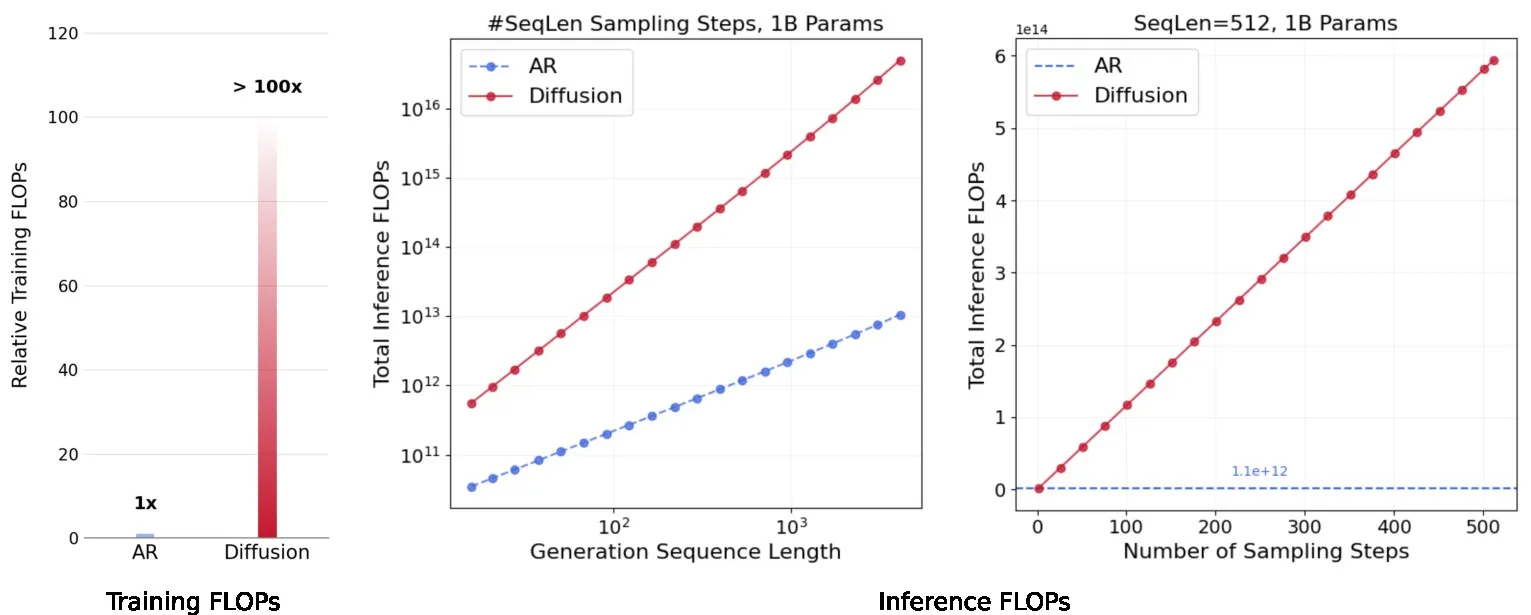
图 F 比较了自回归（AR）和掩码扩散模型在训练和推理过程中的 FLOPs。在训练时，我们的初步实验表明，扩散模型需要比 AR 模型多至少约两个数量级（>100倍）的 FLOPs 才能达到最佳性能，具体数字取决于模型大小和数据预算。在推理时，给定固定的采样步数，掩码扩散模型每个任务消耗的 FLOPs 是 AR 模型的16倍到4700倍，并且这个差距随着目标序列长度从16增加到4096而扩大（图 F 中）。此外，对于恒定的序列长度，扩散模型消耗的 FLOPs 与采样步数成线性关系。理论上，扩散模型可以在单步内生成一个 N-词元的序列，而 AR 模型则天生需要 N 个顺序步骤。然而，由于 KV 缓存机制的存在，AR 模型生成 N 个词元的计算成本大致相当于扩散模型执行单步采样的成本。值得注意的是，扩散模型的大部分计算可以并行化。因此，在实践中，只要未达到 GPU 的计算瓶颈，在相同采样步数下，扩散模型和 AR 模型之间的推理速度差距仍然是可以接受的。此外，专门为计算密集型工作负载优化的 GPU 架构的进步，可能在不久的将来进一步缩小这一性能差距。

回顾大型语言模型的历史，许多近期的智能飞跃，如 T5 [3]、GPT-3 [13] 和 o1 [14]，都是 FLOPs 扩展的直接结果。相信 FLOPs 之神！

2.2 自回归模型为计算效率牺牲了数据潜力

自回归（AR）建模方法（即 Transformer 架构结合教师强制和因果掩码）是人工智能历史上一个传奇般的局部最优解。其成功可归结为两个因素：

• 对现代 GPU 架构的优化利用： AR 在训练期间实现了极高的信噪比（signal-to-FLOPs ratio），并在批量推理期间实现了高的模型 FLOPs 利用率（MFU）。在训练时，一个批次中的每个词元都能持续接收到梯度信号，其期望信号量大约是采用线性调度策略的掩码扩散模型的两倍。确实，很难找到在信噪比效率上超越 AR 的其他方法。在推理时，逐词元生成的方式天然地促进了像连续批处理（continuous batching）这样的吞吐量优化技术，从而最大化了 MFU。因此，AR 是一个极其稳健且高效的基线方法。
• 自然语言可以用较低的损失进行因果建模： 经验表明，在网络规模的语料库上进行预训练时，因果（从左到右）建模总能比其他序列顺序获得更低的损失（参见文献 [12] 的图2）。如果必须为语言建模选择一种单一的序列顺序，因果顺序在经验上是最佳的（公式3），因为它有效地捕捉了自然语言的模式。这也很容易解释：大多数文本数据是由人类生成的，而人类就像是循环神经网络（RNNs）。然而，如前所述，纯粹的因果建模天生会错过某些上下文依赖关系，这表明其在数据潜力方面仍有提升空间。

当前，一个新兴的趋势是计算资源正变得日益廉价，这使得智能扩展的主要瓶颈转向了数据可用性。因此，对于那些致力于推动前沿智能的研究者来说，以往对最大化 GPU 利用率的强调已经减弱。由因果掩码施加的内在建模局限性，现在正变得不可接受。这激励了我们对 DLMs 的探索，它们有意牺牲计算效率以换取更高的数据效率——这代表了一种与自回归方法截然相反的路径。

为了在这两个极端之间寻求一个有利的平衡点，一个自然的策略是进行插值，如块扩散方法（block diffusion methods）[15] 所例。然而，要实现可比的训练效率仍然充满挑战：块扩散方法天生要求每个生成的块都以一个干净的上下文为条件，这与自回归训练中采用的高效的教师强制范式相比，极大地限制了训练效率。

2.3 损失函数告诉我们要重复数据

当对掩码 DLMs 进行多轮次训练时，我们实际上是将每个唯一的原始数据点转换成了多个带有噪声的变体。具体来说，掩码扩散模型的损失函数包含一个期望项 ，该项位于负对数似然部分之外。在这里， 表示在扩散时间步 ，根据前向加噪过程，由干净输入 条件化的掩码序列 的分布。直观地讲，这意味着在每个时间步 ，对所有可能的掩码配置 的损失进行平均。

换句话说，该目标函数明确要求预训练数据集中的每个数据点，在多种掩码率和组合下被破坏，以便通过估计一个更精确的期望来进行更有效的训练。 因此，数据重复的需求是内生地源于扩散模型的目标函数，而非来自某个随意的设定。开源模型，如 LLaDA，通常由于计算资源的限制，对每个数据点仅进行一次加噪，这相当于使用单样本蒙特卡洛估计来近似这个期望项。

3. 《数据受限下，扩散模型击败自回归模型》一文中的主要问题

✨ 本节亮点

1. 首先，我们希望强调，文献 [1] 中的一些结论是有效的，我们在此仅关注其存在问题的方法论和结论。
2. 文献 [1] 的所有实验都使用了一个有问题的损失函数公式，这可能导致误导性的结论。
3. 验证损失不是一个好的用于 AR 和扩散模型比较的指标，因为：

   1. 一个是测量精确的负对数似然，而另一个是其上界。
   2. 如 1.2 节所证，更低的损失并不意味着更好的能力。
4. 文献 [1] 使用了 AR 模型的早期检查点作为其基准结果，导致了不公平的比较。
5. 文献 [1] 在比较 AR 和扩散模型的过拟合趋势时，为 AR 模型使用了更大的模型和更小规模的唯一训练词元——这是一个不公平的设置，因为更大的模型在更多样性不足的数据上训练，天生就更容易提前过拟合。
6. 文献 [1] 中使用的缩放定律假设验证损失是单调不增的，而这在实践中因过拟合导致的损失上升而失效。这个有缺陷的假设导致了拟合效果差，并使任何基于其预测得出的结论带有偏见。

3.1 有问题的比较指标

a. 有问题的扩散损失函数公式

我们注意到，作者在最新的 arXiv 提交版本（v3）中修改了原始草稿，增加了一个线性的时间依赖重加权项。然而，我们将保持假设，即所有实验都使用了公式(1)，因为文献 [1] 中图4(b)的损失范围与公式(1)预期的行为高度匹配。我们期待其代码库的发布（截至本文发布时仍是一个空仓库）以及社区的相关复现工作。

文献 [1] 中的所有实验都采用了以下损失函数，但未给出明确的理由：

该公式可以解释为对期望的掩码词元 的交叉熵损失进行求和。这里 表示句子样本 的第 个元素； 是将干净数据 破坏为在时间步 的噪声数据 的前向过程；而 是由参数 参数化的预测分布。

然而，上述损失函数与理论上更坚实且被广泛采用的掩码扩散语言建模损失有显著不同，后者定义如下：

这个公式是由多个先前的工作，如 SEDD [4]、RADD [5]、MD4 [6] 和 [7] 从理论上推导出来的。同时，它也是当前最先进的 DLMs（如 LLaDA [8]、Dream [9]、[16]、DiffuCoder [10] 等）普遍接受的损失函数。

具体来说，损失函数(1)缺少了时间依赖的重加权项 。理论上，我们可以证明损失(1)并不能忠实地代表模型的似然（详细讨论见 MD4 [6] 论文的 H.4 节）。而损失(2)则被证明是负对数似然的一个上界。

这可能导致文献 [1] 中的结论出现问题。 由于 [1] 的所有实验都基于损失(1)，其每一个结论都可能存在问题，包括交叉点的存在性、交叉点的位置、幂律拟合/预测、关键计算前沿，甚至基准测试结果（其基准结果是根据最佳验证损失选取的，而这种做法本身也是有问题的，稍后会讨论）。

b. 验证损失是比较 AR 和 DLM 的好指标吗？

简短回答： 当损失函数公式有问题时，当然不是，因为它们代表的不是同一个东西；当损失函数公式正确时，仍然不是，因为：

• 一个是测量精确的负对数似然，而另一个是其上界。
• 如 1.2 节所证，更低的损失并不意味着更好的能力。

自回归模型使用交叉熵损失，它通过链式法则计算精确的负对数似然：

然而，掩码 DLMs 计算的是负对数似然的一个上界 [5, 6, 16]，如公式(2)和下式所示：

将一个精确的似然值与一个上界进行比较，这在根本上是有缺陷的，会导致有偏的结论。

此外，如 1.2 节所讨论，更低的验证损失并不必然意味着下游任务性能的提升。 如图 E 所示，由于过拟合，验证损失在某个点之后会上升，而基准性能在训练结束前却持续提升。 因此，文献 [1] 中许多完全依赖于验证损失得出的结论，在根本上是有问题的。

3.2 有问题的 AR 与扩散模型比较实验设置

a. 所呈现的 AR 基准结果远非最佳

文献 [1] 的表2呈现了“具有最佳验证损失的模型”的结果。根据 [1] 的 4.4 节所述，扩散模型“未观察到收敛迹象”，这意味着所报告的扩散模型结果对应于最终的训练检查点。相比之下，自回归（AR）模型在训练早期就表现出验证损失的上升，导致 [1] 选择了一个早期的检查点。 正如我们在 1.2 节中详细阐述的，即使在验证损失开始上升后，AR 模型的基准指标仍在持续改善，这表明所报告的 AR 结果是次优的，因此使得该比较显著不公平。图 G 使用我们自己实验的训练曲线来说明了这种差异。

文献 [1] 基于其图4和图5做出了以下论断，声称：

“随着重复次数的增加，AR 模型会过拟合，显示出发散的损失曲线。相比之下，扩散模型在不同重复次数下表现出重叠的曲线，表明没有过拟合迹象，并且数据重用带来的衰减率非常低。”

以及

“我们发现，对于 AR 模型，重复数据带来的好处几乎等同于新数据，但仅限于大约4个轮次。超过此点，额外的重复会产生递减的收益。相比之下，扩散模型在高达100个轮次内仍然能匹配唯一数据曲线，这表明在数据受限的情况下，它们从重复数据中获益的能力要大得多。”

然而，用于证实这些说法的实验设置存在根本性缺陷。 如图 E 所示，增加模型大小或减少训练数据集中的唯一词元会显著加速过拟合的发生。然而，文献 [1] 中的图4和图5为 AR 模型设置了远大于 Diffusion 模型的规模和更少的唯一词元，这使得比较在根本上是不公平的。即使使用相同的架构，正如在 1.3 节中详细阐述的，更大的模型规模加上更少的唯一训练词元，不可避免地会导致过早的过拟合。更多细节已在上述图的标题中提供。

3.3 有问题的缩放定律拟合方法

遵循文献 [11]，文献 [1] 训练了不同规模和数据预算的 AR 和掩码 DLMs，以拟合以下的损失函数形式：

其中 和 分别表示模型参数和数据集大小；, , , , , , 是通过训练数据点拟合的系数。 和 表示考虑了收益递减的“有效参数和数据集大小”。

很容易验证， 相对于 和 是单调不增的，这一条件隐含地对验证损失的形状施加了一个限制性假设。然而，正如文献 [11] 的图4和本文的图 E 所示，这个假设并非总能成立（文献 [11] 的 F 节也注意到了这一点但未解决）。 具体来说，由于模型对训练数据的过拟合，验证损失可能会上升，这使得任何从损失公式(5)的预测中得出的结论都带有偏见。例如，文献 [1] 图5中观察到的关于轮次数的单调趋势在现实中永远不会发生，而图6中展示的预测可能同样被高估了。

此外，文献 [1] 忽略了另一个关键方面：尽管掩码扩散模型对数据重复表现出鲁棒性，但长时间的训练最终仍会导致过拟合和验证损失的上升，正如前面 1.3 节所讨论的。

结语

本篇博客提供了强有力的证据，表明 DLMs 是超级数据学习者，在固定的唯一数据预算下能实现远为更高的数据效率——这使它们成为一个极具前景的架构范式。文章进一步探讨了 DLMs 与 AR 模型之间的实践权衡，并提供了有据可依的见解。此外，它还评析了同期研究中的方法论缺陷，指出了关键的错误来源，旨在提供更可靠的结论，以启发和推动未来的研究。

我强烈鼓励社区发布更多批判性的博客，作为一种更有效的“开放式评审”。尤其是在传统会议评审日益失去公信力的今天，稳健而透明的社区反馈对于推动科学——不仅仅是人工智能——走向更健康、更严谨的标准至关重要。

References

[1] Prabhudesai, Mihir, et al. "Diffusion Beats Autoregressive in Data-Constrained Settings." arXiv preprint arXiv:2507.15857 (2025, version 2).

[2] Su, Dan, et al. "Nemotron-CC: Transforming Common Crawl into a refined long-horizon pretraining dataset." arXiv preprint arXiv:2412.02595 (2024).

[3] Raffel, Colin, et al. "Exploring the limits of transfer learning with a unified text-to-text transformer." Journal of machine learning research 21.140 (2020): 1-67.

[4] Lou, Aaron, Chenlin Meng, and Stefano Ermon. "Discrete diffusion modeling by estimating the ratios of the data distribution." arXiv preprint arXiv:2310.16834 (2023).

[5] Ou, Jingyang, et al. "Your absorbing discrete diffusion secretly models the conditional distributions of clean data." arXiv preprint arXiv:2406.03736 (2024).

[6] Shi, Jiaxin, et al. "Simplified and generalized masked diffusion for discrete data." Advances in neural information processing systems 37 (2024): 103131-103167.

[7] Sahoo, Subham, et al. "Simple and effective masked diffusion language models." Advances in Neural Information Processing Systems 37 (2024): 130136-130184.

[8] Nie, Shen, et al. "Large language diffusion models." arXiv preprint arXiv:2502.09992 (2025).

[9] Ye, Jiacheng, et al. “Dream 7B.” https://hkunlp.github.io/blog/2025/dream (2025)

[10] Gong, Shansan, et al. "DiffuCoder: Understanding and Improving Masked Diffusion Models for Code Generation." arXiv preprint arXiv:2506.20639 (2025).

[11] Muennighoff, Niklas, et al. "Scaling data-constrained language models." Advances in Neural Information Processing Systems 36 (2023): 50358-50376.

[12] Xue, Shuchen, et al. "Any-Order GPT as Masked Diffusion Model: Decoupling Formulation and Architecture." arXiv preprint arXiv:2506.19935 (2025).

[13] Brown, Tom, et al. "Language models are few-shot learners." Advances in neural information processing systems 33 (2020): 1877-1901.

[14] OpenAI. "Introducing OpenAI o1” https://openai.com/o1/ (2025)

[15] Arriola, Marianne, et al. "Block diffusion: Interpolating between autoregressive and diffusion language models." arXiv preprint arXiv:2503.09573 (2025).

[16] Nie, Shen, et al. "Scaling up masked diffusion models on text." arXiv preprint arXiv:2410.18514 (2024).

[17] Khanna, Samar, et al. "Mercury: Ultra-Fast Language Models Based on Diffusion." arXiv e-prints (2025): arXiv-2506.

[18] Google DeepMind. “Gemini Diffuson.” https://blog.google/technology/google-deepmind/gemini-diffusion/. https://blog.google/technology/google-deepmind/gemini-diffusion/ (2025)

[19] ByteDance Seed. “Seed Diffusion: A Large-Scale Diffusion Language Model with High-Speed Inference.” "https://lf3-static.bytednsdoc.com/obj/eden-cn/hyvsmeh7uhobf/sdiff_updated.pdfj” (2025)

[20] Xue, Fuzhao, et al. "To repeat or not to repeat: Insights from scaling llm under token-crisis." Advances in Neural Information Processing Systems 36 (2023): 59304-59322.

[21] https://x.com/mihirp98/status/1948875821797798136

译自：https://jinjieni.notion.site/Diffusion-Language-Models-are-Super-Data-Learners-239d8f03a866800ab196e49928c019ac