在众多大模型测试时扩展(Test-time Scaling)方法中,基于采样的(sampling-based)方法因其简单、通用且效果显著而成为主流。这类方法的基本流程是:针对一个给定的输入,多次调用模型进行采样,生成多条不同的推理路径(reasoning paths),然后通过一个特定的机制来评估这些路径的“置信度”(confidence),最终选择置信度最高的路径所对应的答案。其中,最具代表性的两种置信度评估机制分别是“自洽性”(Self-Consistency, SC)和“困惑度”(Perplexity, PPL)。
自洽性(Self-Consistency):它通过生成多个推理路径,然后采用“投票”的方式来决定最终答案。在所有生成的答案中,出现次数最多的那个被认为是最终的正确答案。这种方法的置信度评估是基于最终答案之间的一致性,而非推理过程本身。
困惑度(Perplexity):它利用 LLM 在生成每个词元(token)时给出的条件概率,计算整条推理路径的概率或困惑度。直观上,一条模型更确信的路径(即概率更高、困惑度更低)被认为更有可能是正确的。
尽管这些基于采样的技术在实践中取得了广泛的成功,但它们背后的理论基础却一直未能得到充分的探讨。使得我们无法从根本上解释为什么在某些场景下 SC 表现更好,而在另一些场景下 PPL 更优。只能通过实验观察到现象,例如 SC 在采样预算有限时性能不佳,但无法从理论上定位其瓶颈所在。在没有理论指导的情况下,新方法的提出更多地依赖于直觉和试错,缺乏系统性的改进路径。
来自南京大学在 NeurIPS 2025 会议上发表的论文《A Theoretical Study on Bridging Internal Probability and Self-Consistency for LLM Reasoning》首次为分析基于采样的测试时扩展方法提供了一个统一的理论框架。他们创造性地将 LLM 的推理错误分解为两个正交的组成部分,对 SC 和 PPL 进行了剖析,揭示了它们各自的优势与不足。更重要的是,基于这些理论洞见,他们提出了一种新的混合方法——RPC(Reasoning-pruning Perplexity Consistency),该方法不仅在理论上弥补了现有方法的缺陷,更在广泛的实验中得到了验证。

-
论文标题:A Theoretical Study on Bridging Internal Probability and Self-Consistency for LLM Reasoning -
论文链接:https://arxiv.org/pdf/2510.15444
1. 推理错误的分解
在深入探讨具体方法之前,我们首先需要一个可以用来评估和比较不同推理策略优劣的统一标准。他们将 LLM 在推理任务上的整体“推理错误”(Reasoning Error)分解为了两个相互独立的组成部分:估计误差(Estimation Error) 和 模型误差(Model Error)。
让我们首先对问题进行形式化定义。给定一个推理问题,输入为 ,真实答案为 。LLM 通过一系列词元的采样生成一条推理路径 ,并从 中通过一个提取函数 得到最终答案 。例如,在数学题中, 可能是“1+1=2,所以答案是2”,而 就是“2”。
一个理想的置信度评估机制应该能够准确地估计出任意一个答案 是正确答案的概率,我们记这个真实的置信度为 。然而,在实践中,我们无法遍历所有可能的推理路径来计算这个真实值,只能通过采样 条路径 来得到一个估计的置信度 。
论文将推理性能的衡量标准定义为估计置信度与真实标签之间的平方误差,其期望值为:
其中, 是一个指示函数,当 是正确答案 时,其值为 1,否则为 0。
1.1 误差分解
这篇工作的核心在于,上述的推理错误 并非一个不可分割的整体。通过引入真实的(但通常无法获得的)置信度 作为中间量,可以将误差分解为两部分。
命题 1 (误差分解) :对于任意输入 ,真实答案 和任意可能的答案 ,其推理错误可以被分解为:
这个分解公式是整个理论框架的基础。它清晰地揭示了推理错误的两个来源:
-
估计误差 (Estimation Error) :这部分误差衡量了我们基于有限样本的“估计置信度” 与“真实置信度” 之间的差距。这个误差的大小完全取决于我们的采样规模 和我们所采用的置信度估计策略(例如 SC 或 PPL)。它反映了估计过程的稳定性和准确性。当采样数量 趋向于无穷大时,估计误差会趋向于零。
-
模型误差 (Model Error) :这部分误差衡量了 LLM 通过其内在概率分布所能给出的“最佳置信度” 与“理想置信度” 之间的差距。这个误差与采样规模 无关,它是由 LLM 自身的能力和我们定义的置信度度量本身所决定的。它反映了模型对问题理解的深度和置信度度量的有效性。即使我们有无限的采样资源,这部分误差也无法被消除,它代表了当前模型和评估方法所能达到的性能上限。
1.2 分解框架的意义
这个分解框架的价值在于它提供了一个清晰的分析路径。要提升 LLM 的推理性能,我们有两个明确的方向:
-
降低估计误差:我们可以通过增加采样数量 ,或者设计出更高效的置信度估计方法,使得估计误差能够以更快的速度收敛到零。 -
降低模型误差:我们可以通过提升 LLM 自身的能力(例如通过更好的训练),或者设计出更贴近真实问题结构的置信度度量,来缩小模型给出的概率与事实之间的差距。
有了这个分析工具,我们就可以对现有的方法进行一次评估,看看它们各自在这两个误差项上表现如何,从而找到它们的问题所在。
2. SC 与 PPL 的理论分析
2.1 自洽性 (Self-Consistency)
自洽性 (SC) 是一种基于一致性的方法。它通过蒙特卡洛估计来计算一个答案的置信度。具体来说,采样 条路径,得到 个答案,答案 的置信度被估计为它在所有答案中出现的频率:
将 SC 的置信度估计代入通用的误差分解框架,经过推导,可以得到 SC 的推理错误。
命题 2 (SC 推理错误分解) :对于 SC 方法,其推理错误可以分解为:
这个公式揭示了 SC 的几个关键特性:
-
无偏估计:SC 的估计是无偏的,即 。这意味着它的模型误差项与通用框架中的定义完全相同。 -
估计误差的线性收敛:SC 的估计误差项为 。可以看到,这个误差随着采样数量 的增加而线性下降,其收敛速度为 。
SC 的核心局限:线性收敛速度太慢。这意味着为了将估计误差降低到一个足够小的水平,SC 需要大量的样本。在实际应用中,LLM 的推理成本高昂,采样预算通常是有限的。当 较小时,SC 的估计误差会很大,导致其性能不佳。这就从理论上解释了为什么 SC 在小样本场景下效果往往不理想。
2.2 困惑度 (Perplexity)
与 SC 不同,困惑度 (PPL) 方法直接利用 LLM 的内部概率 来评估置信度。由于无法访问所有路径,它只考虑在 次采样中实际出现的路径集合 。对于一条被采样到的路径 ,其估计置信度就是模型给出的原始概率 ;对于未被采样到的路径,其估计置信度为 0。
对 PPL 进行类似的误差分解分析,可以得到其推理错误。
命题 3 (PPL 推理错误分解) :对于 PPL 方法,针对某条路径 的推理错误可以分解为:
这个公式揭示了 PPL 的几个重要特性:
-
估计误差的指数收敛:PPL 的估计误差项中包含一个因子 。这意味着它的估计误差是随着采样数量 的增加而指数级下降的。相比于 SC 的线性收敛,这是一个巨大的优势。对于那些模型比较确信的路径(即 较大),PPL 能够用少量的样本就快速获得一个准确的置信度估计。
PPL 的两大局限:
-
高模型误差:PPL 的置信度评估是基于单条路径的,它没有利用不同路径可能产生相同答案这一结构性信息。SC 通过对最终答案进行投票,实际上是利用了这种“多对一”的映射关系,从而获得了更低的模型误差。论文在附录中通过一个理想化的例子证明,SC 的模型误差通常小于 PPL。 -
估计误差收敛性的退化:PPL 估计误差的指数收敛速度严重依赖于路径的真实概率 。当一条路径的概率非常低时(), 这一项的收敛优势就会减弱甚至消失。
三、 Reasoning-pruning Perplexity Consistency (RPC)
基于上述的理论分析,论文设计了一种名为“推理剪枝的困惑度一致性”(Reasoning-pruning Perplexity Consistency, RPC)的新方法。RPC 由两个核心组件构成:困惑度一致性 (Perplexity Consistency, PC) 和 推理剪枝 (Reasoning Pruning, RP) ,分别用于解决前面分析出的两个和三个挑战中的前两个和最后一个。
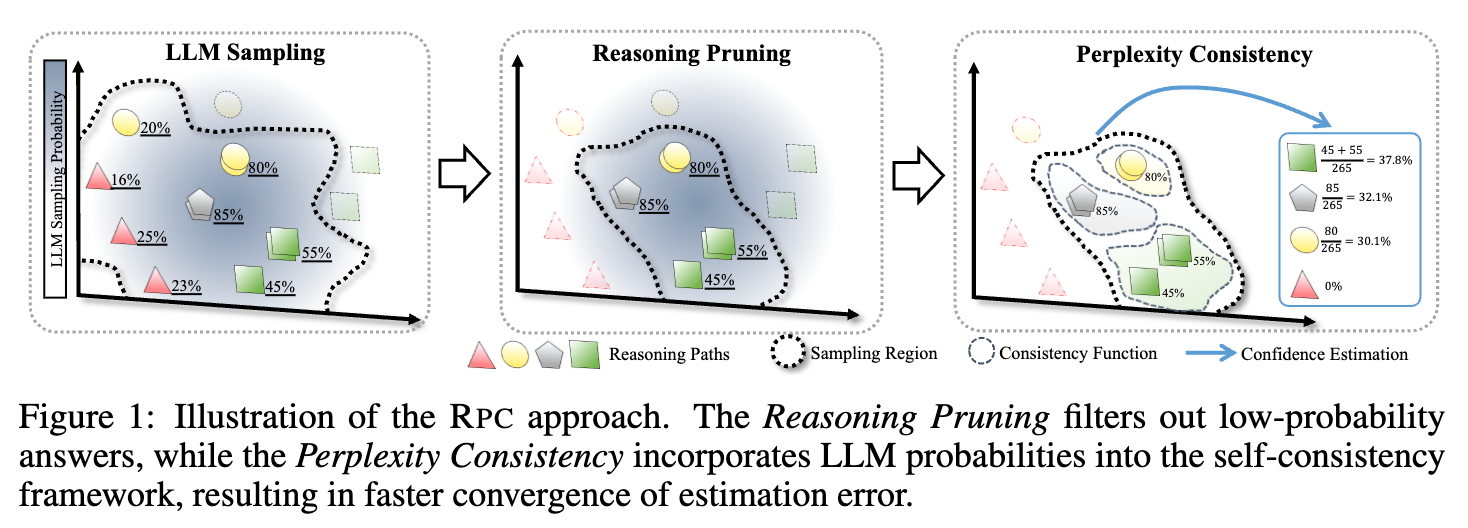
上图直观地展示了 RPC 的工作流程。首先,通过 LLM 采样得到一批带有内部概率的推理路径。然后,“推理剪枝”模块会过滤掉那些低概率的路径。最后,“困惑度一致性”模块在剩余的路径上计算每个答案的最终置信度。
3.1 困惑度一致性 (Perplexity Consistency, PC)
PC 组件的目标是融合 SC 和 PPL 的优点,即同时实现低模型误差和快速的估计误差收敛。它的设计非常直观:用 PPL 的方式加权,用 SC 的方式投票。
具体来说,对于任意一个可能的答案 ,PC 不再是简单地计算其出现频率,而是将所有能够推导出该答案的、且被采样到的路径的模型内部概率进行累加:
其中 是被采样到的不重复路径的集合。这个公式巧妙地结合了 PPL 的内部概率信息和 SC 的答案一致性思想。
对 PC 进行误差分解分析,可以得到以下定理。
定理 4 (PC 推理错误分解) :假设所有能够导出答案 的路径的真实概率之和为 ,并定义 (这里是导出的路径总数,为简化理解可近似看作一个与相关的量),PC 的推理错误可以分解为:
这个定理揭示了 PC 的优越性:
-
低模型误差:PC 的模型误差项与 SC 完全相同,都是 。这意味着它继承了 SC 在利用答案一致性方面的优势,能够获得较低的模型误差。 -
指数收敛的估计误差:PC 的估计误差项中包含一个因子 。由于 是一个小于 1 的值,这保证了其估计误差能够像 PPL 一样实现指数级收敛。
通过这种设计,PC 成功地解决了 SC 的效率问题和 PPL 的高模型误差问题。然而,它仍然面临 PPL 的另一个困境:收敛退化。从定理中可以看到,收敛速度依赖于 的大小。当一个正确答案对应的所有路径的累积概率 非常小时, 会趋近于 1,指数收敛的优势就会退化为线性收敛。
3.2 推理剪枝 (Reasoning Pruning, RP)
RP 组件的目标是解决 PC 在低概率答案上的收敛退化问题。其核心思想是:一个累积概率极低的答案,本身就不太可能是正确答案,我们可以直接将其“剪掉”,从而避免在其上浪费计算资源和引入不必要的估计误差。
具体来说,RP 会设置一个阈值 。当一个答案 的估计累积概率 小于这个阈值时,就直接将其置信度设为 0,相当于从候选答案中移除。
这引出了两个关键问题:
-
剪枝的有效性:这样做会不会错误地将正确的答案剪掉,从而反而增加了模型误差? -
阈值的确定:如何自动地、非启发式地确定一个合适的阈值 ?
论文对这两个问题都给出了理论和实践上的解答。
剪枝的有效性(理论保证)
定理 7 (推理路径剪枝的有效性) :论文证明,如果将阈值 设置为真实答案 的概率 ,那么 RP 能够以一个很高的概率实现最优的错误削减。
这个定理从理论上保证了,只要阈值设置得当,剪枝操作不仅不会损害性能,反而能有效地降低整体推理错误,因为它同时优化了估计误差和模型误差。
阈值的自动确定(实践方法)
在实践中,我们无法知道真实答案的概率 。因此,需要一个自动化的方法来确定剪枝的范围。论文借鉴了开集识别(open-set recognition)领域的思想,提出了一种基于概率分布建模的方法。
该方法假设所有采样到的路径的内部概率 来自一个由两个分布混合而成的模型:一个代表“高概率区域”,另一个代表“低概率区域”。论文选择使用两个威布尔分布 (Weibull distribution) 的混合来对这个概率分布进行建模:
其中 是威布尔分布的概率密度函数, 是混合权重。
对于一个具体的推理问题,首先收集所有 条采样路径的概率值,然后使用最大似然估计来拟合上述混合模型的参数。拟合完成后,对于任意一条新的路径 ,我们就可以计算它属于“高概率”分布的后验概率 。
剪枝规则如下:
-
移除所有属于低概率区域的路径,即满足 的路径。 -
为了增加在小样本量下的稳定性,额外使用截断均值法(Truncated Mean method),保留所有概率大于全体路径概率均值的路径。
通过这种方式,RP 能够自动地识别并剔除那些“异常”的低概率路径,而无需任何手动设置的超参数。这使得整个 RPC 方法变得鲁棒且易于使用。
4. 实验
论文在一系列具有挑战性的基准测试上对 RPC 进行了全面的评估,旨在回答以下三个核心问题(RQ):
-
RQ1: 效率 (Efficiency) :相比于基准方法(特别是 SC),RPC 能否用更少的样本达到同等甚至更好的性能? -
RQ2: 效果 (Efficacy) :在相同的采样预算下,RPC 的性能是否优于现有方法? -
RQ3: 可靠性 (Reliability) :RPC 给出的置信度估计是否比其他方法更可靠、更接近于真实的准确率?
4.1 实验设置
-
数据集:实验涵盖了数学推理和代码生成两大类任务。 -
数学推理:包括四个高难度基准:MATH, MathOdyssey, OlympiadBench, 和 AIME。 -
代码生成:包括三个常用基准:HumanEval, MBPP, 和 APPS。
-
-
模型:使用了多种不同规模和架构的模型,如 InternLM2-Math-Plus (1.8B, 7B), DeepSeekMath-RL (7B), 和 Deepseek-Coder (33B)。 -
对比方法:主要与 PPL, SC, 以及另一种基于语言探针的“口头置信度”(Verbalized Confidence, VERB)方法进行比较。
4.2 实验结果分析
RQ1: 效率
为了验证效率,实验比较了 PC 和 RPC 达到 SC 最佳性能所需的最小样本数量。
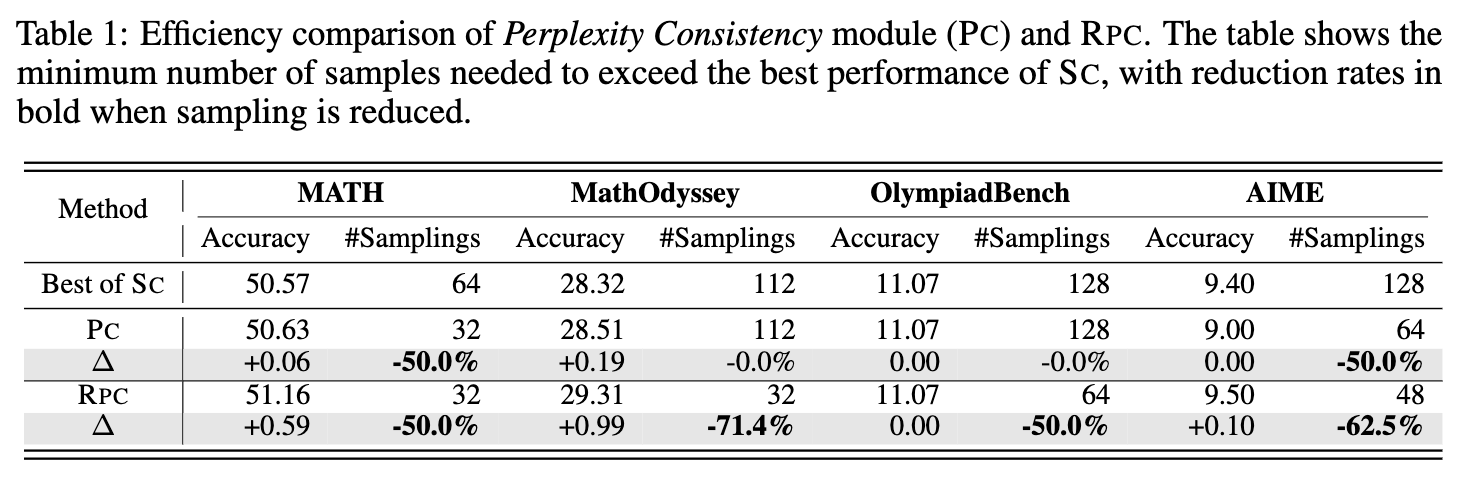
从上表可以看出,RPC 的效率提升是显著的。
-
在 MATH 和 AIME 数据集上,RPC 仅用 SC 50% 的样本量就达到了超越 SC 的性能。 -
在 MathOdyssey 和 AIME 上,RPC 更是将样本需求降低了 71.4% 和 62.5% 。 -
单独的 PC 组件虽然也能在部分数据集上降低样本需求,但其效果不如完整的 RPC,这说明了 RP 组件在解决收敛退化问题上的重要性。
这些结果有力地支持了理论分析:RPC 的指数级收敛特性使其在样本效率上远超线性收敛的 SC。
RQ2: 效果
为了验证效果,实验比较了在不同采样数量 下,各个方法的准确率。
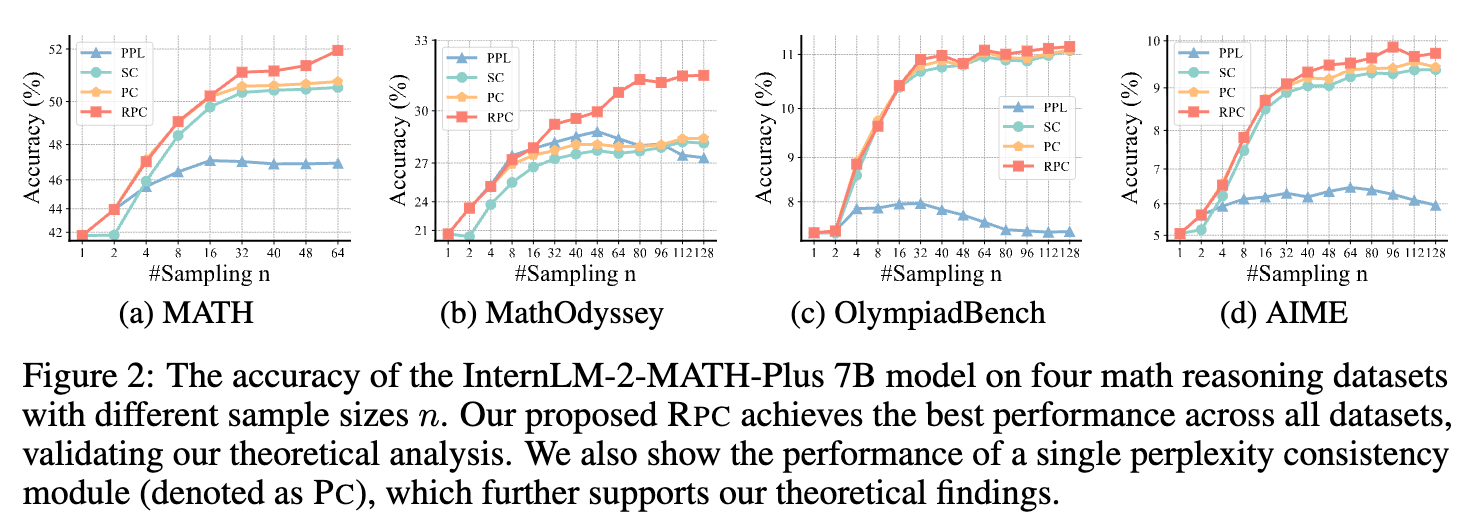
上图展示了在四个数学推理数据集上,随着采样数量增加,各方法性能的变化曲线。可以清晰地看到:
-
RPC(红色曲线)在几乎所有的采样点上都取得了最佳性能,全面优于 SC(绿色曲线)和 PPL(蓝色曲线)。 -
PC(橙色曲线)的性能通常介于 RPC 和 SC 之间,并且其收敛速度明显快于 SC,验证了理论分析中 PC 拥有更快收敛速度的结论。 -
从 PC 到 RPC 的性能提升(尤其是在 MATH 和 MathOdyssey 数据集上),再次证明了 RP 模块通过剪除低质量路径来降低模型误差的有效性。
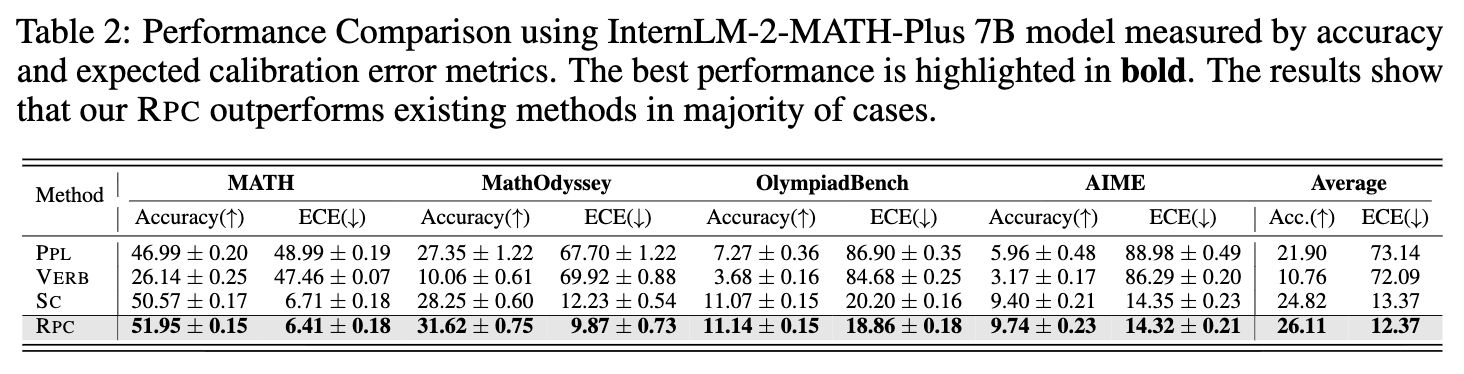
上表提供了在最大采样预算下,各方法的平均准确率(Accuracy)和预期校准误差(ECE)的详细数据。在四个数据集的平均准确率上,RPC (26.11%) 显著高于 SC (24.82%) 和 PPL (21.90%),展示了其较强的综合性能。
RQ3: 可靠性
一个好的置信度估计方法,不仅要能帮助模型选出正确答案(提升准确率),其输出的置信度分数本身也应该是有意义的。例如,如果模型对一批答案给出的平均置信度是 80%,那么这批答案的实际准确率也应该在 80% 左右。预期校准误差(ECE)是衡量这种可靠性的标准指标,ECE 值越低,说明置信度越可靠。
从上面的表 2 中可以看到:
-
RPC 在所有四个数据集上的平均 ECE 值 (12.37) 是最低的,远低于 SC (13.37) 和 PPL (73.14)。这表明 RPC 产生的置信度分数与模型的实际表现最为吻合。
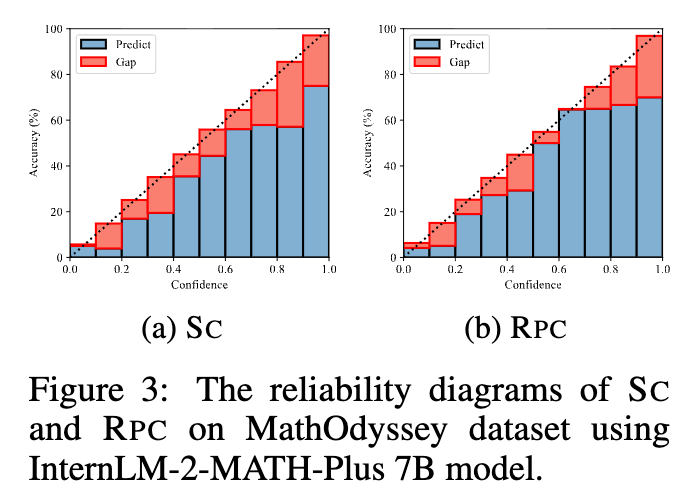
上图是 SC 和 RPC 在 MathOdyssey 数据集上的可靠性图。图中的蓝色条形代表每个置信度区间内模型的实际准确率,虚线代表理想的完美校准线。可以看到,RPC 的蓝色条形更贴近虚线,尤其是在高置信度区间,其“缺口”(Gap)远小于 SC。这直观地展示了 RPC 在置信度校准上的优势。
4.3 泛化性与鲁棒性分析
除了上述核心实验,论文还进行了一系列补充实验来验证 RPC 的泛化能力:
-
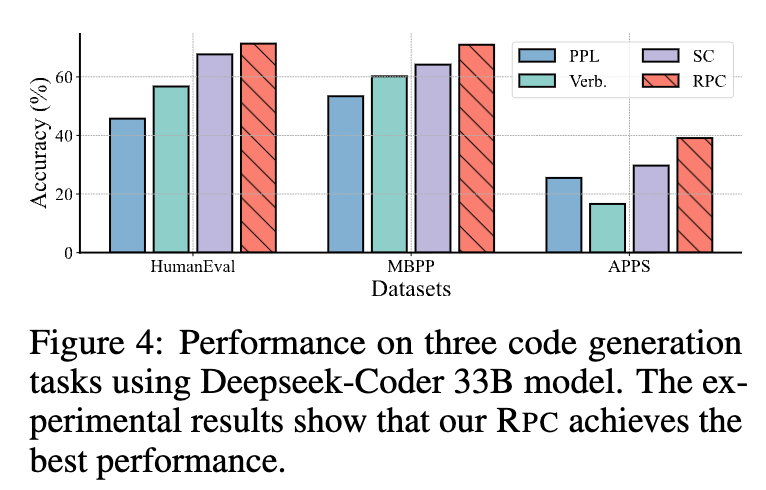
跨任务泛化:在代码生成任务上,RPC 同样取得了最佳性能(见图 4)。 -
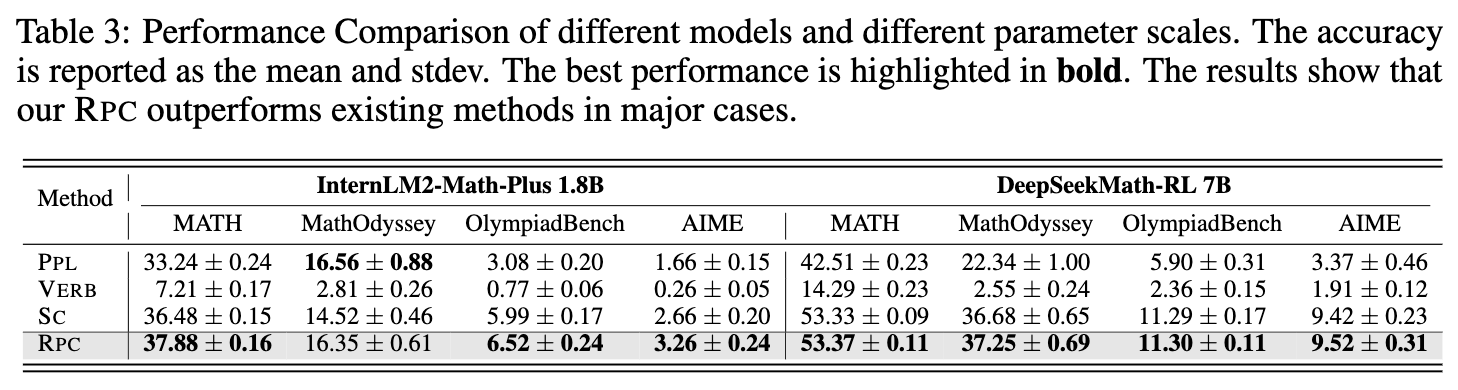
跨模型泛化:在不同规模(1.8B vs 7B)和不同架构(InternLM vs DeepSeek)的模型上,RPC 的优势保持一致(见表 3)。 -
与先进方法的兼容性:将 RPC 的思想与更先进的 SC 变体(如 ESC)和 PPL 变体(如使用奖励模型的 Best-of-N)结合,RPC 依然能带来稳定的性能提升。 -
计算开销分析:理论和实践分析都表明,RPC 引入的额外计算开销(主要是混合模型拟合)与 LLM 推理本身的时间相比可以忽略不计。考虑到它能大幅减少所需的推理样本数,RPC 实际上提供了一种计算效率更高的选择。
5. 实践启示
本文最大的亮点是首次提出了一个系统性分析“基于采样的测试时扩展方法”的理论框架。将推理错误分解为估计误差(Estimation Error)和模型误差(Model Error)。为领域内长久以来依赖直觉和经验的做法填补了理论空白。
RPC 的核心优势之一是用更少的样本达到比 SC 更好的性能。
当你的模型效果不佳时,RPC也可以帮你高效评估模型问题,是出在估计误差上,还是模型误差上:
将你的采样数量 n 翻倍(例如从 10 增加到 20)。
如果性能有显著提升,说明你当前的主要瓶颈是估计误差。这意味着你的采样数量不足,继续增加样本或改用 RPC 这样的高效估计方法是正确的优化方向。
如果性能提升甚微甚至没有变化,说明你的主要瓶颈是模型误差。这意味着当前的基座模型能力已经到顶了,再怎么增加采样也无济于事。此时,你应该考虑的是更换一个更强大的模型、对当前模型进行微调或优化你的 Prompt。
往期文章:




