在现代数据科学中,许多数据结构都可以表示为图,如互联网、社交网络等。这些图结构中的数据为机器学习提供了丰富的理论和应用场景。其中,PageRank 算法是图链接分析的经典代表,它是图数据上的无监督学习方法的典范。
PageRank 算法最初由 Larry Page 和 Sergey Brin 在 1996 年提出。这个算法的诞生背后有一个有趣的故事。当时,两人都是斯坦福大学的研究生,他们认为互联网上的链接结构可以为页面的重要性提供线索。这与当时主流的基于关键词的搜索方法形成了鲜明的对比。他们的这一洞察力不仅为他们赢得了学术界的赞誉,更为他们后来创建的 Google 搜索引擎奠定了基础。
尽管 PageRank 最初是为互联网页面设计的,但其核心思想可以广泛应用于任何有向图结构。事实上,随着时间的推移,PageRank 已被用于多种应用,如社会影响力分析、文本摘要生成等。
PageRank 的核心思想是基于有向图上的随机游走模型,这是一个一阶马尔可夫链。该模型描述了一个随机游走者如何沿着图的边随机移动,从一个节点访问到另一个节点。在满足某些条件的前提下,这个随机游走过程最终会收敛到一个平稳分布。在这个平稳分布中,每个节点被访问的概率即为其 PageRank 值,这个值可以被解释为节点的重要性。值得注意的是,PageRank 是递归定义的,这意味着一个页面的 PageRank 值部分地取决于链接到它的其他页面的 PageRank 值。因此,计算 PageRank 值通常需要迭代方法。
1. PageRank的定义
1.1 基本想法
在互联网的早期历史中,PageRank 算法被引入作为一种评估网页重要性的方法。简而言之,PageRank 是一个定义在整个网页集合上的函数,为每个网页分配一个正实数,代表该网页的重要性。这些数值组成一个向量,其中较高的 PageRank 值意味着该网页在重要性上的优势,因此在搜索结果中可能会被优先显示。
可以将整个互联网视为一个巨大的有向图,其中每个网页是一个节点,而超链接则是从一个页面指向另一个页面的有向边。基于这个视角,我们可以构建一个随机游走模型,也就是一阶马尔可夫链。在这个模型中,我们假设一个虚拟的网页浏览者会随机地、按照等概率地跟随一个页面上的任何一个超链接到另一个页面,并持续这种随机跳转。在长时间内,这种随机跳转的行为会形成一个稳定的模式,即马尔可夫链的平稳分布。每个网页的 PageRank 值,实际上就是在这个平稳分布中的概率。
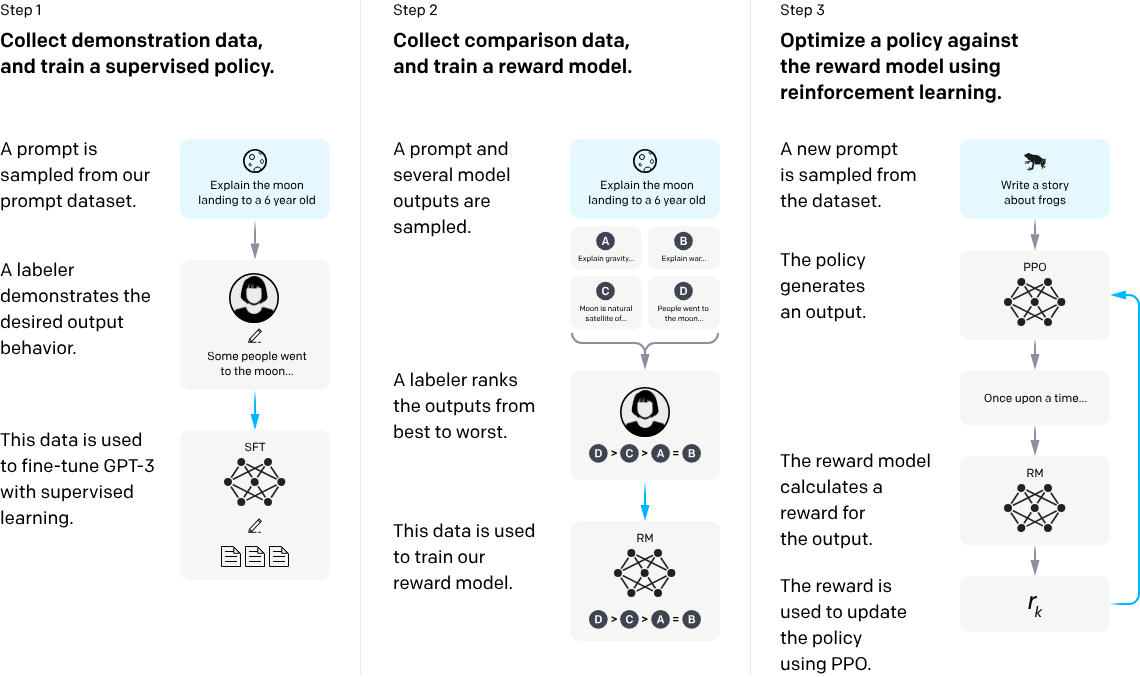
举一个简单的例子:假设有三个网页 A、B 和 C。A 链接到 B 和 C,B 只链接到 C,而 C 只链接到 A。在随机游走模型中,从 A 出发的浏览者有 50% 的概率跳转到 B 或 C;从 B 出发的浏览者会 100% 跳转到 C;而从 C 出发的浏览者则会 100% 跳转到 A。经过多次迭代,我们会发现 C 的 PageRank 值可能会比 A 和 B 都高,因为它接收到了 A 和 B 的流量。这就是 PageRank 如何帮助我们量化网页重要性的简化示例。
直观上,一个网页,如果指向该网页的超链接越多,随机跳转到该网页的概率也就越高,该网页的PageRank值就越高,这个网页也就越重要。一个网页,如果指向该网页的PageRank值越高,随机跳转到该网页的概率也就越高,该网页的PageRank值就越高,这个网页也就越重要。PageRank值依赖于网络的拓扑结构,一旦网络的拓扑(连接关系)确定,PageRank值就确定。
PageRank 的计算可以在互联网的有向图上进行,通常是一个迭代过程。先假设一 个初始分布,通过迭代,不断计算所有网页的PageRank值,直到收敛为止。
下面首先给出有向图及有向图上随机游走模型的定义,然后给出PageRank的基本定义,以及PageRank的一般定义。基本定义对应于理想情况,一般定义对应于现实情况。
1.2 有向图和随机游走模型
1.2.1 有向图
有向图(Directed Graph)是图论中的一个基本概念,由节点(Vertices)和有向边(Directed Edges or Arcs)组成。在有向图中,每条边都有一个起始节点和一个终止节点,表示方向从起始节点指向终止节点。
有向图G可以定义为一个二元组G=(V, E),其中:
- V是一个非空的有限集合,代表图中的节点。
- E是一个有序对的子集,即 E \subseteq V \times V,代表图中的有向边。对于每一条有向边(u, v),其中u是起始节点,v是终止节点。
在互联网中,每个网页可以被视为有向图中的一个节点。当一个网页中包含指向另一个网页的超链接时,可以将这个超链接视为从第一个网页(起始节点)指向第二个网页(终止节点)的有向边。
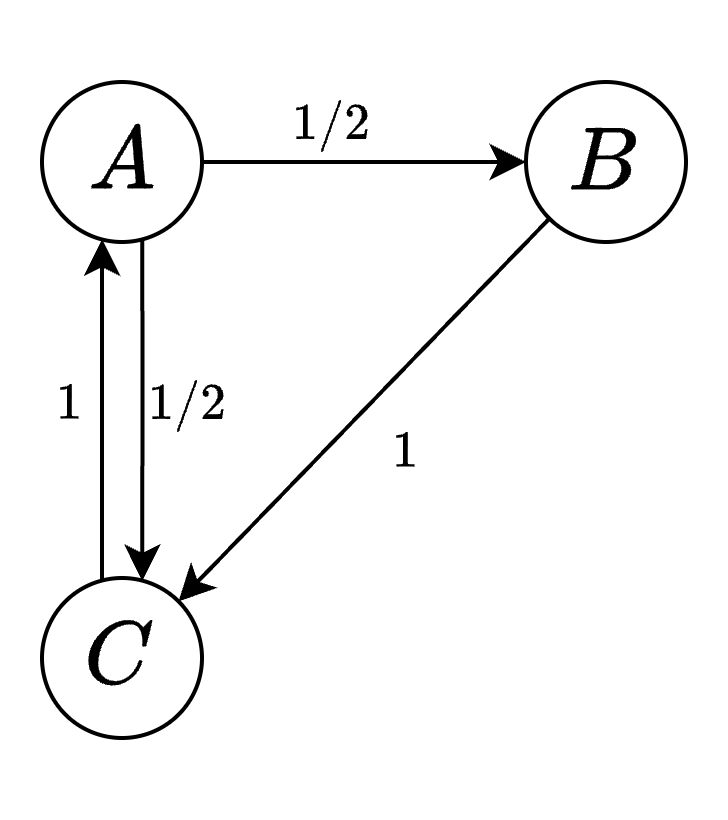
例如,假设我们有三个网页:A、B 和 C。
- 网页 A 包含指向网页 B 和网页 C 的链接。
- 网页 B 包含指向网页 C 的链接。
- 网页 C 包含指向网页 A 的链接。
在这个例子中,我们可以将这三个网页视为有向图的三个节点,而它们之间的超链接关系构成了有向边。因此,有向图的边集合为:E = \{(A, B), (A, C), (B, C), (C, A)\}。
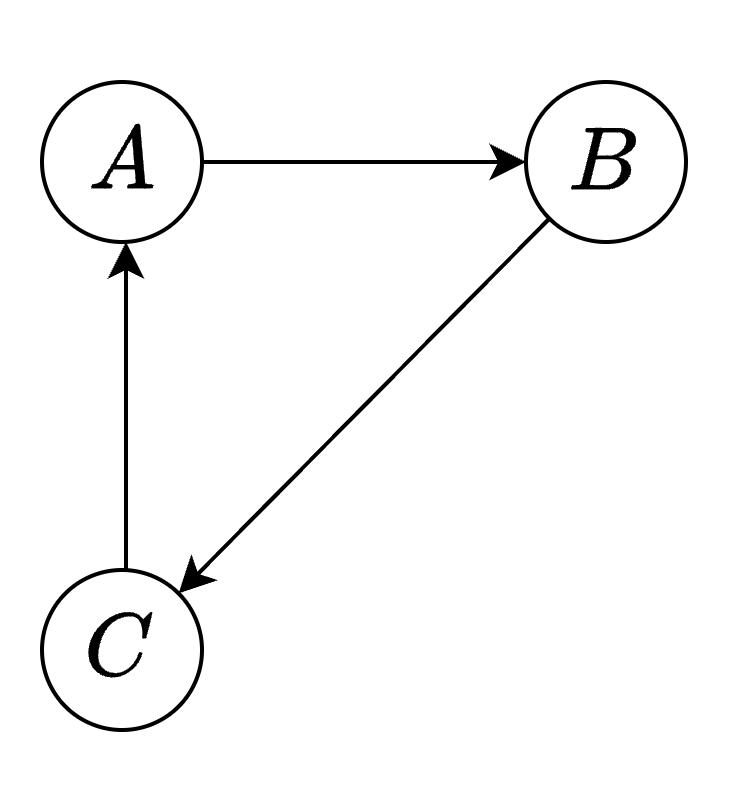
下图是一个周期性有向图的例子。从结点A出发返回到A,必须经过路径A-B-C-A,所有可能的路径的长度都是3的倍数,所以结点A是周期性结点,这个有向图是周期性图。
1.2.2 随机游走模型
给定一个含有n个结点的有向图,在有向图上定义随机游走(random walk)模型,即一阶马尔可夫链,其中结点表示状态,有向边表示状态之间的转移,假设从一个结点到通过有向边相连的所有结点的转移概率相等。具体地,转移矩阵是一个n阶矩阵
M=[m_{ij}]_{n \times n}\tag{1}第i行第j列的元素m_{ij}取值规则如下:如果结点j有k个有向边连出,并且结点i是其连出的一个结点,则m_{ij}=1/k;否则m_{ij}=0。
注意转移矩阵具有性质:
m_{ij} \ge 0 \tag{2} \sum\limits_{i = 1}^n {{m_{ij}} = 1} \tag{3}即每个元素非负,每列元素之和为1即矩阵M为随机矩阵(stochastic matrix)。
在有向图上的随机游走形成马尔可夫链。也就是说,随机游走者每经一个单位时间转移一个状态,如果当前时刻在第i个结点(状态),那么下一个时刻在第j个结点(状态)的概率是m_{ij}这一概率只依赖于当前的状态,与过去无关,具有马尔可夫性。
1.3 PageRank的基本定义
给定一个包含n个结点的强连通且非周期性的有向图,在其基础上定义随机游走模型。假设转移矩阵为M,在时刻0,1,2, \cdots ,t, \cdots,访问各个结点的概率分布为
{R_0},M{R_0},{M^2}{R_0}, \cdots ,{M^t}{R_0}, \cdots\tag{4}则极限
\mathop {\lim }\limits_{t \to \infty } {M^t}{R_0} = R\tag{5}存在,极限向量R表示马尔可夫链的平稳分布,满足
MR=R\tag{6}平稳分布R称为这个有向图的 PageRank。 R的各个分量称为各个结点的PageRank值。
R=\left[\begin{array}{c} P R\left(v_{1}\right) \\ P R\left(v_{2}\right) \\ \vdots \\ P R\left(v_{n}\right) \end{array}\right]其中
P R\left(v_{i}\right)=\sum_{v_{j} \in M\left(v_{i}\right)} \frac{P R\left(v_{j}\right)}{L\left(v_{j}\right)}, \quad i=1,2, \cdots, n\tag{7}这里M(v_i)表示指向结点v_i的结点集合,L(v_j)表示结点v_j连出的有向边的个数。
1.4 PageRank的一般定义
为了考虑到用户不仅会通过点击链接来浏览网页,还可能随机选择一个网页。因此需要在基本定义的基础上导入平滑项阻尼因子。阻尼因子d取值由经验决定,例如d=0.85。当d接近1时,随机游走主要依照转移矩阵M进行;当d接近0时,随机游走主要以等概率随机访问各个结点。
\begin{align} R& = (dM+\frac {1-d} n \mathbf E)R\\ & = dMR+\frac {1-d} n \mathbf 1 \end{align}\tag{8}也就是
P R\left(v_{i}\right)=d\left(\sum_{v_{j} \in M\left(v_{i}\right)} \frac{P R\left(v_{j}\right)}{L\left(v_{j}\right)}\right)+\frac{1-d}{n}, \quad i=1,2, \cdots, n\tag{9}2. PageRank的实现
实现 PageRank 算法的一个简单方法是使用 Python 和 NumPy。以下是一个基本的 PageRank 实现:
这个实现使用了迭代方法来计算 PageRank。M 是转移概率矩阵,其中 M[i][j] 是从页面 j 到页面 i 的转移概率。
注意:在实际应用中,网页的数量可能非常大,因此可能需要更高效的方法和数据结构来处理大规模的数据。此外,为了确保 M 是随机矩阵,可能需要进行一些预处理步骤,例如处理挂起节点(没有出链的节点)。